HDU1402 - A * B Problem Plus
题目链接
大数乘法是多项式的基础应用,其原理是将多项式 f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + ⋯ + a n x n f(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots+a_nx^n f(x)=a0+a1x+a2x2+a3x3+⋯+anxn中的 x = 10 x=10 x=10,然后让大数的每一位当做对应的 1 0 y 10^y 10y的系数,然后进行多项式乘法运算,以降低大数乘法的时间复杂度(高精度乘法时间复杂度是 O ( n 2 ) O(n^2) O(n2)的,多项式乘法是 O ( n log n ) O(n\log n) O(nlogn), n n n是位数)。
在进行多项式乘法之后,我们得到了新的多项式 h ( x ) = c 0 + c 1 × 10 + c 2 × 1 0 2 + ⋯ + c m × 1 0 m h(x)=c_0+c_1\times 10+c_2\times 10^2+\cdots + c_m\times 10^m h(x)=c0+c1×10+c2×102+⋯+cm×10m。
这里的 c 0 , c 1 , ⋯ , c m c_0,c_1,\cdots,c_m c0,c1,⋯,cm由于在乘法时会发生进位,所以每一位可能会大于 9 9 9,此时要将后面的位的值挪到下一位上去,让这一位保证在 9 9 9以内。
然后从高位到低位找到第一个不是 0 0 0的位,然后逐位输出即可。
如果最终结果是 0 0 0,要特别判断。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = (1ll << 47) * 7 * 4451 + 1;
const LL g = 3;LL mul(LL x, LL y) {return (x * y - (LL)(x / (long double)mod * y + 1e-3) * mod + mod) % mod;
}template<class T> T power(T a, LL b) {T res = 1;for (; b; b >>= 1) {if (b & 1) res = mul(res, a);a = mul(a, a);}return res;
}LL rev[4000005];void change(LL *y, int len) {for (int i = 0; i < len; ++i) {if (i < rev[i]) swap(y[i], y[rev[i]]);}
}void DFT(LL *y, int len, int on) {change(y, len);for (LL h = 2; h <= len; h <<= 1) {LL wn = power(g, (mod - 1) / h);if (on == -1) wn = power(wn, mod - 2); for (int j = 0; j < len; j += h) {LL w = 1ll;for (int k = j; k < j + h / 2; ++k) {LL u = y[k] % mod;LL t = mul(w, y[k + h / 2]);y[k] = (u + t) % mod;y[k + h / 2] = (u - t + mod) % mod;w = mul(w, wn);}}}
}void NTT(LL *x1, LL *x2, LL len) {for (int i = 0; i < len; ++i) {rev[i] = rev[i >> 1] >> 1;if (i & 1) rev[i] |= len >> 1;}DFT(x1, len, 1);DFT(x2, len, 1);for (int i = 0; i < len; ++i) {x1[i] = mul(x1[i], x2[i]);}DFT(x1, len, -1);LL inv = power(len, mod - 2);for (int i = 0; i < len; ++i) {x1[i] = mul(x1[i], inv);}
}string a, b;
LL x1[2000005], x2[2000005];void main2() {cin >> b;int n = a.length(), m = b.length();int len = 1;while (len <= (n + m) * 2 + 1) len <<= 1;int pt = n - 1;for (char c: a) {x1[pt--] = c - '0';}for (int i = n; i < len + 300; ++i) {x1[i] = 0;}pt = m - 1;for (char c: b) {x2[pt--] = c - '0';}for (int i = m; i < len; ++i) {x2[i] = 0;}NTT(x1, x2, len);for (int i = 0; i < len; ++i) {if (x1[i] > 9) {x1[i + 1] += (x1[i] / 10);x1[i] %= 10;}}pt = len;while (x1[pt] > 0) {if (x1[pt] > 9) {x1[pt + 1] += (x1[pt] / 10);x1[pt++] %= 10;}}while (pt >= 0 and x1[pt] == 0) --pt;if (pt == -1) {cout << 0 << '\n';return;}for (int i = pt; i >= 0; --i) {cout << x1[i];}cout << '\n';
}int main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);LL _ = 1;
// cin >> _;while (cin >> a) main2();return 0;
}
HDU4609 - 3-idiots
题目链接
要求能够成三角形的概率,我们可以通过可以构成三角形的情况总数/总的情况数来得到。其中总的情况数就是 ( n 3 ) \binom{n}{3} (3n),重点是求解可以构成三角形的情况。
首先我们可以维护一个多项式, x i x_i xi的系数表示长度为 i i i的线段有多少条。那么以样例 1 1 1为例,得到的多项式的系数就是: [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1] [0,1,0,2,1]。
接下来,我们将这个多项式自己与自己相乘,也就是 [ 0 , 1 , 0 , 2 , 1 ] × [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1]\times [0,1,0,2,1] [0,1,0,2,1]×[0,1,0,2,1],得到的多项式的系数是: [ 0 , 0 , 1 , 0 , 4 , 2 , 4 , 4 , 1 ] [0,0,1,0,4,2,4,4,1] [0,0,1,0,4,2,4,4,1]。
这个多项式表示的含义是从第一个 [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1] [0,1,0,2,1]取出一个边,从第二个 [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1] [0,1,0,2,1]取出一个边:
取出两个边的长度和为 0 0 0的有 0 0 0种;
取出两个边的长度和为 1 1 1的有 0 0 0种;
取出两个边的长度和为 2 2 2的有 1 1 1种;
取出两个边的长度和为 3 3 3的有 0 0 0种;
取出两个边的长度和为 4 4 4的有 4 4 4种;
取出两个边的长度和为 5 5 5的有 2 2 2种;
取出两个边的长度和为 6 6 6的有 4 4 4种;
取出两个边的长度和为 7 7 7的有 4 4 4种;
取出两个边的长度和为 8 8 8的有 1 1 1种。
我们现在要利用得到的这个信息来求解答案。
我们先来看一看我们的三条边形成三角形,有怎样的条件:设三角形三条边是 a , b , c a,b,c a,b,c,且 a < b < c a<b<c a<b<c。于是有 a + b > c a+b>c a+b>c。
首先,在我们得到的 [ 0 , 0 , 1 , 0 , 4 , 2 , 4 , 4 , 1 ] [0,0,1,0,4,2,4,4,1] [0,0,1,0,4,2,4,4,1]中,存在同一条边被采用两次的情况,首先我们要遍历每一条边,将长度之和为其二倍的情况 − 1 -1 −1。原始的 4 4 4条边的边长分别是 [ 1 , 3 , 3 , 4 ] [1,3,3,4] [1,3,3,4],所以我们要减去两条边长度为 [ 2 , 6 , 6 , 8 ] [2,6,6,8] [2,6,6,8]的一种方案。于是变成: [ 0 , 0 , 0 , 0 , 4 , 2 , 2 , 4 , 0 ] [0,0,0,0,4,2,2,4,0] [0,0,0,0,4,2,2,4,0]。
然后,由于我们两边的边是一样的,左边取 a a a右面取 b b b,左边取 b b b右边取 a a a,这两种其实应当是一种方案。所以我们应当将每一个可能的两边长度的可能情况减半。于是变成 [ 0 , 0 , 0 , 0 , 2 , 1 , 1 , 2 , 0 ] [0,0,0,0,2,1,1,2,0] [0,0,0,0,2,1,1,2,0]。
如果我们设最终答案为 t o t a l total total,将卷积后得到的结果求一个前缀和叫做 p r e pre pre, n n n条边最长的那条边为 m x mx mx。先将所有边从小到大进行排序。
接下来依次枚举 n n n条边,对于第 i i i条边,我们设其长度为 c i c_i ci,并认定其为最长边的情况,求解这种情况时的可行方案数。首先,根据两边之和大于第三边,我们剩下两条边的长度之和应当大于 c i c_i ci,所以从刚刚卷积和处理后得到的信息中,将长度之和为 [ c i + 1 , ∞ ] [c_i+1,\infty] [ci+1,∞]的可能情况加到答案中。
那么这一步就是 t o t a l ← t o t a l + p r e [ 2 m x ] − p r e [ c i ] total\leftarrow total+pre[2mx]-pre[c_i] total←total+pre[2mx]−pre[ci]。
然后根据我们刚才所设,当前边我们令其为最大边,所以一切包含一个小于 c i c_i ci的边、包含一个大于 c i c_i ci的边都是不合法的,但是因为这两条边的长度和一定大于 c i c_i ci,所以被算进了 t o t a l total total里面,所以要从 t o t a l total total里面减掉。我们考虑这样的可能发生情况是 ( n − i ) × ( i − 1 ) (n-i)\times (i-1) (n−i)×(i−1),其中 n − i n-i n−i是比 c i c_i ci长的边的数量, i − 1 i-1 i−1是比 c i c_i ci短的数量和。
这一步就是 t o t a l ← t o t a l − ( n − i ) × ( i − 1 ) total\leftarrow total-(n-i)\times(i-1) total←total−(n−i)×(i−1)。
还有一种情况,就是两条边都取了比 c i c_i ci长的,那就是 ( n − i 2 ) \binom{n-i}{2} (2n−i)种情况,因为是从比 c i c_i ci长的 n − i n-i n−i个边里任意挑选两个边。
这一步就是 t o t a l ← t o t a l − ( n − i 2 ) total\leftarrow total-\binom{n-i}{2} total←total−(2n−i)。
还有一种情况,就是一条边取了自身,另一条边取了其他,存在 n − 1 n-1 n−1种情况。这里因为之前已经除以 2 2 2,所以不用考虑从哪里搬来的情况。
这一步就是 t o t a l ← t o t a l − ( n − 1 ) total\leftarrow total-(n-1) total←total−(n−1)。
将 n n n条边对 t o t a l total total的贡献全部计算一遍之后,最后的结果就是所有合法的情况数了。
最后的答案就是 t o t a l ( n 3 ) \frac{total}{\binom{n}{3}} (3n)total。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100005;
const LL mod = 998244353;
const LL g = 3, gi = 332748118;
const double PI = acos(-1.0);struct Complex {double x, y;Complex(double _x = 0.0, double _y = 0.0) {x = _x; y = _y;}Complex operator - (const Complex &b) const {return Complex(x - b.x, y - b.y);}Complex operator + (const Complex &b) const {return Complex(x + b.x, y + b.y);}Complex operator * (const Complex &b) const {return Complex(x * b.x - y * b.y, x * b.y + y * b.x);}
};LL rev[4000005];void change(Complex *y, int len) {for (int i = 0; i < len; ++i) {if (i < rev[i]) swap(y[i], y[rev[i]]);}
}void FFT(Complex *y, int len, int on) {change(y, len);for (int h = 2; h <= len; h <<= 1) {Complex wn(cos(2 * PI / h), sin(on * 2 * PI / h));for (int j = 0; j < len; j += h) {Complex w(1, 0);for (int k = j; k < j + h / 2; ++k) {Complex u = y[k];Complex t = w * y[k + h / 2];y[k] = u + t;y[k + h / 2] = u - t;w = w * wn;}}}if (on == -1) {for (int i = 0; i < len; ++i) {y[i].x = y[i].x / len + 0.5;}}
}LL n, len = 289999;
LL a[N], x[N * 3], pre[N * 2];
Complex F[N * 2];void main2() {cin >> n;LL mx = 0;memset(x, 0, sizeof(x));for (int i = 1; i <= n; ++i) {cin >> a[i];mx = max(mx, a[i]);++x[a[i]];}len = 1;while (len <= mx * 2 + 1) len <<= 1;for (int i = 0; i <= mx; ++i) {F[i].x = (double)x[i];F[i].y = 0;}for (int i = mx + 1; i < len; ++i) {F[i].x = F[i].y = 0;}for (int i = 0; i < len; ++i) {rev[i] = rev[i >> 1] >> 1;if (i & 1) rev[i] |= len >> 1;}FFT(F, len, 1);for (int i = 0; i < len; ++i) {F[i] = (F[i] * F[i]);}FFT(F, len, -1);for (int i = 0; i < len; ++i) {x[i] = (LL)F[i].x;}for (int i = 1; i <= n; ++i) {--x[a[i] * 2];}for (int i = 1; i <= mx * 2; ++i) {x[i] /= 2;}pre[0] = 0;for (int i = 1; i <= mx * 2; ++i) {pre[i] = pre[i - 1] + x[i];}LL total = 0;for (LL i = 1; i <= n; ++i) {total += (pre[mx * 2] - pre[a[i]]);total -= ((n - i) * (i - 1));total -= (n - 1);total -= ((n - i) * (n - i - 1) / 2);}LL all = n * (n - 1) * (n - 2) / 6;double ans = (double)total / (double)all;cout << fixed << setprecision(7) << ans << '\n';
}int main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);LL _ = 1;cin >> _;while (_--) main2();return 0;
}
CF954I - Yet Another String Matching Problem
题目链接
首先考虑,如果 S S S串和 T T T串长度相同,该怎么做。我们发现,我们的目的是消除差异性,即对于上下每一对字母,他们最后都要变成同一个字母。
以abcd和ddcb为例,那么上下每一对依次是a-d,b-d,c-c,d-b。我们将每一个字母设为一个点,将每一对当做一个边连起来,连完之后长这个样子:
会发现几个字母会连成一个连通图:
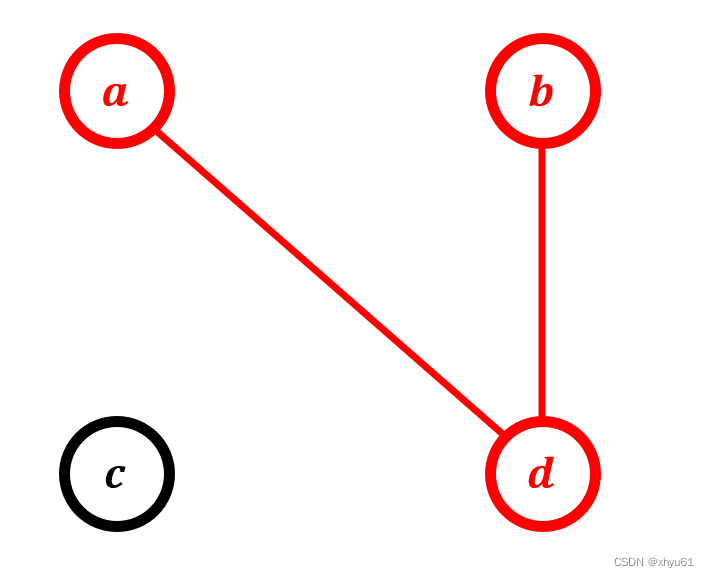
我们将四个字母分为了两个部分: c c c自己是一个部分, a b d abd abd三个字母是一个部分。我们发现,连的边指在原来的两个串中对应的同一个位置的两个字母,他们最终要变成同一个字母。而每一次操作要同时改变两个串中的这个字母,所以我们不难推出,被我们连上边形成连通块的这些字母,他们最后必然要变成同一个字母。我们就让他变成他们之中的一个字母,那么我们发现,其实我们的操作数,就是我们连的边的数量,因为我们每连一次边,就相当于要进行一次题目中的操作,变换一个字母。
这样我们用并查集来实现:对于每一个位置,判断这个位置的两个字母是否相同,如果相同那就不需要我们动了;如果不同,就需要判断这两个字母现在是否在一个连通块,如果在,则不管(已经变成同样的字母了),不在同一个连通块就用并查集合并一下,然后答案 + 1 +1 +1。
因为我们的字符集只有前 6 6 6个字母 a b c d e f abcdef abcdef,所以合并操作这类的都是常数级别。那么,在两个串长度相等的情况下,得到答案的时间复杂度是 O ( m ) O(m) O(m)的。
但是我们原题中 S S S串会比较长,我们需要枚举每一个长度为 ∣ T ∣ \vert T\vert ∣T∣的子串,每个子串都要求一次答案,于是时间复杂度变成 O ( n m ) O(nm) O(nm)的了,直接爆炸。
我们来尝试进行一波优化,看看哪里是最消耗时间的地方。
我们注意到,我们的字符串长度的规模是 1.25 × 1 0 5 1.25\times 10^5 1.25×105,而我们的字符集大小只有 6 6 6,意味着我们同一个位置可能的字符对只有 6 × 36 6\times 36 6×36种。又由于我们不考虑上下相同的字符串,所以我们需要考虑的字符对情况只有 36 − 6 = 30 36-6=30 36−6=30种。对于一次子串和 T T T串的求解过程中,如果串过长,那么相同的字符对会出现很多次,而其中只有一次是有用的,在第一次的时候我们对这两个字母进行连边,从第二次开始再遇到这个字符对,根本就是毫无用处了。所以,如果我们能够判断出,每一个子串跟 T T T串匹配的过程中,所有位里是否包含这样的字符对就好了。
怎么来做?先说结论:用到卷积。
先来看一个关于卷积的性质。假设我们有两个多项式:
f ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n f(x)=a0+a1x+a2x2+⋯+anxn
g ( x ) = b 0 + b 1 x + b 2 x 2 + ⋯ + b n x n g(x)=b_0+b_1x+b_2x^2+\cdots+b_nx^n g(x)=b0+b1x+b2x2+⋯+bnxn
试求 f ( x ) ⋅ g ( x ) f(x)\cdot g(x) f(x)⋅g(x)。
我们发现, f ( x ) ⋅ g ( x ) = a 0 b 0 + ( a 0 b 1 + a 1 b 0 ) x + ( a 0 b 2 + a 1 b 1 + a 2 b 0 ) x 2 + ( a 0 b 3 + a 1 b 2 + a 2 b 1 + a 3 b 0 ) x 3 + ⋯ f(x)\cdot g(x)=a_0b_0+(a_0b_1+a_1b_0)x+(a_0b_2+a_1b_1+a_2b_0)x^2+(a_0b_3+a_1b_2+a_2b_1+a_3b_0)x^3+\cdots f(x)⋅g(x)=a0b0+(a0b1+a1b0)x+(a0b2+a1b1+a2b0)x2+(a0b3+a1b2+a2b1+a3b0)x3+⋯
发现了什么?最后得到的多项式系数, x k x^k xk的系数是 ∑ i = 0 k a i b k − i \displaystyle\sum\limits_{i=0}^k a_ib_{k-i} i=0∑kaibk−i,你会发现他们由所有 i + j = k i+j=k i+j=k的 a i b j a_ib_j aibj相加得到,换句话说,组成 x k x^k xk的系数的所有 a i b j a_ib_j aibj,都满足他们的下标和 i + j i+j i+j是定值,且定值为 k k k。
然后看看我们需要的是什么?事实上,我们可以总结出我们现阶段的问题是:从 S S S串的第 i i i位作为第一个字符的长度为 ∣ T ∣ \vert T\vert ∣T∣的子串和 T T T串匹配的过程中,字符 c 1 c_1 c1和字符 c 2 c_2 c2是否出现。
在其中的一个固定了 c 1 c_1 c1和 c 2 c_2 c2的子问题中,我们设一个数组 a i a_i ai,表示 S S S串的第 i i i位是否为 c 1 c_1 c1。如果 a i = 1 a_i=1 ai=1,说明是 c 1 c_1 c1;如果 a i = 0 a_i=0 ai=0,说明第 i i i不是 c 1 c_1 c1。同样的方式设一个数组 b i b_i bi,表示 T T T串第 i i i位是否为 c 2 c_2 c2。
那么, T T T串的第一个字母和 S S S串第 i i i个字母对上的时候,字符对 ( c 1 , c 2 ) (c1,c2) (c1,c2)出现的条件是什么?如果 ∑ k = 0 ∣ T ∣ − 1 a i + k b k > 0 \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k}>0 k=0∑∣T∣−1ai+kbk>0,说明存在这样的字符对 ( c 1 , c 2 ) (c_1,c_2) (c1,c2)。
因为这种情况下, S S S串的第 i + k i+k i+k位和 T T T串的第 k k k是对上的,只有 a i + k = b k = 1 a_{i+k}=b_k=1 ai+k=bk=1成立,我们才能说这样的字符对存在。
但是怎么求呢?我们现在有了 a i , b i a_i,b_i ai,bi,但是因为 ∑ k = 0 ∣ T ∣ − 1 a i + k b k \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k} k=0∑∣T∣−1ai+kbk中 a , b a,b a,b的下标加起来不是一个常值。如果是一个常值的话,我们就可以把 a i a_i ai数组和 b i b_i bi数组当做两个多项式的系数,然后我们进行多项式的乘法,这时 a i b j a_ib_j aibj自然就是我们两个多项式乘在一起之后 x i + j x^{i+j} xi+j的系数中的一部分。
我们发现,我们要求的这个求和公式的形式等同于 ∑ k = 0 ∣ T ∣ − 1 a i b j \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_ib_j k=0∑∣T∣−1aibj,如果 i + j i+j i+j是定值 C C C,那么我们所求的求和公式的结果就是多项式乘在一起之后 x C x^C xC的系数。
观察我们想求的公式 ∑ k = 0 ∣ T ∣ − 1 a i + k b k \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k} k=0∑∣T∣−1ai+kbk,我们发现,如果 b k b_k bk中的 k k k变成 − k -k −k,哪怕是加一点常数,就完美了。因为这样两个变量 k k k就抵消掉了,剩下的和就是一个定值,就可以通过两个多项式相乘之后的系数求得。
把 b k b_k bk中的 k k k变成 − k -k −k很简单,我们可以直接将 T T T串翻转,这样我们原本的 b k b_k bk就变成了 b ∣ T ∣ − k − 1 b_{\vert T \vert-k-1} b∣T∣−k−1,我们原本要求的求和公式 ∑ k = 0 ∣ T ∣ − 1 a i + k b k \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k} k=0∑∣T∣−1ai+kbk也变成了 ∑ k = 0 ∣ T ∣ − 1 a i + k b ∣ T ∣ − k − 1 \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{\vert T\vert-k-1} k=0∑∣T∣−1ai+kb∣T∣−k−1。
这个时候我们 a , b a,b a,b的下标之和就是 ∣ T ∣ + i − 1 \vert T\vert+i-1 ∣T∣+i−1。这里面 ∣ T ∣ \vert T\vert ∣T∣是 T T T的长度,是定值; i i i是当前子问题中 T T T串第一个字符跟 S S S串的哪个字符对齐,在子问题中也是一个定值。于是 ∣ T ∣ \vert T\vert ∣T∣就是一个定值。这样的话,我们就可以利用我们刚刚推出的结论来求解这个求和式了。将两个数组 a , b a,b a,b当做多项式系数后,进行多项式乘法,得到的结果多项式中, x ∣ T ∣ + i − 1 x^{\vert T\vert+i-1} x∣T∣+i−1的系数,就是我们所求的结果。如果这个结果大于 0 0 0,则说明存在这样的字符对 ( c 1 , c 2 ) (c_1,c_2) (c1,c2)。
设 f [ i ] [ c 1 ] [ c 2 ] f[i][c_1][c_2] f[i][c1][c2]为在 T T T串第一个字符跟 S S S串的哪个字符对齐时是否存在字符对 ( c 1 , c 2 ) (c_1,c_2) (c1,c2)。如果存在,其值为 1 1 1,否则为 0 0 0。
所以整体的流程就是:
- 对于字符 c 1 c_1 c1,我们先看 S S S串中哪些位置是 c 1 c_1 c1。设数组 a a a来表示这个信息。如果 a i = 1 a_i=1 ai=1,说明字符串 S S S的第 i i i位是 c 1 c_1 c1;如果 a i = 0 a_i=0 ai=0,说明字符串的第 i i i位不是 c 1 c_1 c1。
- 翻转字符串 T T T。
- 对于字符 c 2 c_2 c2,我们先看 T T T串中哪些位置是 c 2 c_2 c2。设数组 b b b来表示这个信息。如果 b i = 1 b_i=1 bi=1,说明字符串 T T T的第 i i i位是 c 2 c_2 c2;如果 b i = 0 b_i=0 bi=0,说明字符串的第 i i i位不是 c 2 c_2 c2。
- 把得到的 a , b a,b a,b数组当做两个多项式的系数,进行卷积。
- 得到的结果多项式的系数中,如果 0 ≤ ∣ T ∣ + i − 1 < n 0\leq \vert T\vert + i -1 < n 0≤∣T∣+i−1<n,那么只要 x ∣ T ∣ + i − 1 x^{\vert T\vert +i-1} x∣T∣+i−1的系数大于 0 0 0,则可以认为 f [ i ] [ c 1 ] [ c 2 ] = 1 f[i][c_1][c_2]=1 f[i][c1][c2]=1。如果这一项的系数为 0 0 0,则 f [ i ] [ c 1 ] [ c 2 ] = 0 f[i][c_1][c_2]=0 f[i][c1][c2]=0。
这样的话,对于每一对 c 1 , c 2 c_1,c_2 c1,c2,我们都这样操作一遍,就可以得到全部的 f f f数组的信息了,即:我们求得了从 S S S串的第 i i i位作为第一个字符的长度为 ∣ T ∣ \vert T\vert ∣T∣的子串和 T T T串匹配的过程中,字符 c 1 c_1 c1和字符 c 2 c_2 c2是否出现。接下来用这个信息,对于每一个 i i i的位置,看看所有点对的情况,然后用上面说到的方法用并查集合并一下,就得到了每一个位置的答案。
试试分析现在的时间复杂度。多项式乘法采用FFT或者NTT的话,一次DFT/IDFT的时间复杂度是 O ( n log n ) O(n\log n) O(nlogn)。我们一共进行了 30 30 30个两个字母不同的字符对的查询,每一次查询进行了 3 3 3次DFT/IDFT,也就是说光是在多项式乘法上,时间复杂度就是 O ( 30 × 3 n log n ) O(30\times 3 n\log n) O(30×3nlogn)。经过计算发现这个时间复杂度略微有点大。主要原因是 30 × 3 30\times 3 30×3这个常数太大了。
每一个点对都要进行 3 3 3次DFT,这三次 D F T DFT DFT分别做了:
- 将 S S S串的 a a a数组进行DFT
- 将翻转后的 T T T串的 b b b数组进行DFT
- 将得到的结果进行IDFT。
但是,由于我们的字符集是有限大小的,我们每一个字母作为字符对的第一个字母时,都要求一次 a a a数组,进行一次DFT,这是重复操作。 b b b数组也是同理。所以我们可以预处理出 S S S串所有字符的 a a a数组的DFT后的结果,预处理出翻转后 T T T串所有字符的 b b b数组的DFT后的结果。后续求的时候,直接将预处理出的两个数组相乘,然后进行一次IDFT即可。这样,我们进行DFT/IDFT的次数是两个串的 a , b a,b a,b数组DFT预处理 6 + 6 = 12 6+6=12 6+6=12次, 30 30 30个字符对的IDFT 30 30 30次,一共只有 42 42 42次。时间复杂度一下子就砍了一半。
最后求解的时候每一个位置遍历所有字符对 36 36 36个,每一个字符对的操作是常数级(因为字符集很小),所以这个做法整体的时间复杂度可以认为是 O ( 42 n log n + 36 n ) O(42n\log n+36n) O(42nlogn+36n),经过计算,是可以通过本题的。
代码采用NTT。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = (1ll << 47) * 7 * 4451 + 1;
const LL g = 3;
const LL N = 300005;string ss, tt;
LL s[125005], t[125005];
LL f[N][8][8];
LL n, m, c;
LL sa[8][N], ta[8][N];
LL tmp[N];
LL rev[N], fa[8], rk[8];LL mul(LL x, LL y) {return (x * y - (LL)(x / (long double)mod * y + 1e-3) * mod + mod) % mod;
}template<class T> T power(T a, LL b) {T res = 1;for (; b; b >>= 1) {if (b & 1) res = mul(res, a);a = mul(a, a);}return res;
}void change(LL *y, int len) {for (int i = 0; i < len; ++i) {if (i < rev[i]) swap(y[i], y[rev[i]]);}
}void DFT(LL *y, int len, int on) {change(y, len);for (LL h = 2; h <= len; h <<= 1) {LL wn = power(g, (mod - 1) / h);if (on == -1) wn = power(wn, mod - 2); for (int j = 0; j < len; j += h) {LL w = 1ll;for (int k = j; k < j + h / 2; ++k) {LL u = y[k] % mod;LL t = mul(w, y[k + h / 2]);y[k] = (u + t) % mod;y[k + h / 2] = (u - t + mod) % mod;w = mul(w, wn);}}}
}int find(int x) {return ((fa[x] == x) ? x : (fa[x] = find(fa[x])));
}void merge(int i, int j) {int x = find(i), y = find(j);if (rk[x] <= rk[y]) fa[x] = y;else fa[y] = x;if (rk[x] == rk[y] && x != y) ++rk[y];
}void main2() {cin >> ss >> tt;n = ss.length(); m = tt.length();for (int i = 0; i < n; ++i) {s[i] = ss[i] - 'a';sa[s[i]][i] = 1;}for (int i = 0; i < m; ++i) {t[i] = tt[i] - 'a';ta[t[i]][m - i - 1] = 1;}LL len = 1;while (len <= (n + m)) len <<= 1;for (int i = 0; i < len; ++i) {rev[i] = rev[i >> 1] >> 1;if (i & 1) rev[i] |= len >> 1;}for (int i = 0; i < 6; ++i) {DFT(sa[i], len, 1);DFT(ta[i], len, 1);}for (int i = 0; i < 6; ++i) {for (int j = 0; j < 6; ++j) {if (i == j) continue;for (int k = 0; k < len; ++k) {tmp[k] = mul(sa[i][k], ta[j][k]); }DFT(tmp, len, -1);LL inv = power(len, mod - 2);for (int k = 0; k < len; ++k) {tmp[k] = mul(tmp[k], inv);if (k + 1 - m >= 0 and k + 1 - m < n) f[k + 1 - m][i][j] = tmp[k];}}}for (int i = 0; i < n - m + 1; ++i) {for (int j = 0; j < 6; ++j) {fa[j] = j; rk[j] = 1;}int sum = 0;for (int j = 0; j < 6; ++j) {for (int k = 0; k < 6; ++k) {if (j == k or !f[i][j][k]) continue;int fx = find(j), fy = find(k);if (fx != fy) {++sum;merge(fx, fy);}}}cout << sum << ' ';}
}int main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);LL _ = 1;
// cin >> _;while (_--) main2();return 0;
}






![2023年中国体育赛事行业现状及趋势分析:体育与科技逐步融合,推动产业高质量发展[图]](https://img-blog.csdnimg.cn/img_convert/2fc2b3f17b2b5ff4d1b90540be97d9f9.png)