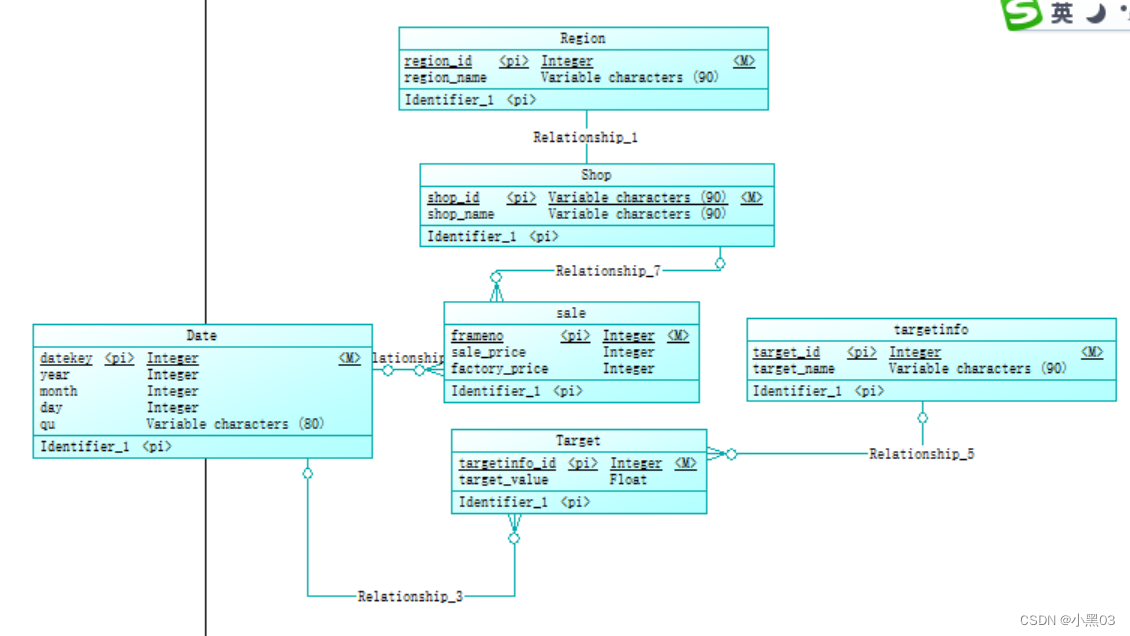
Determinant 一个翻译很不友好的名字 行列式 det(A)

flyfish

determinant
美[dɪ'tɜːrmɪnənt] 
英[dɪ'tɜːmɪnənt] 
adj. 决定性的n. 决定性因素 / <数>行列式 / 决定因素 / 方阵

举一个最简单的例子说明行列式

假设有一个 2x2 矩阵 A：
$A=\left(\begin{array}{cc}2& 1\\ 1& 2\end{array}\right)$

这个矩阵可以被视为一个线性变换，它将平面上的向量从原始位置（输入区域）变换到新位置（输出区域）。

步骤

1. 我们首先绘制变换前的单位正方形（面积为 1）。
2. 使用矩阵 A 变换这个单位正方形，得到一个平行四边形（面积为行列式的绝对值）。
3. 计算矩阵 A 的行列式，确认这个比例。

Python代码

以下是使用Python绘制变换前后的区域，并计算行列式的代码：

import numpy as np
import matplotlib.pyplot as pltdef plot_transformation(matrix, ax, title):# 原始单位正方形的四个顶点square = np.array([[0, 0],[1, 0],[1, 1],[0, 1],[0, 0]])# 变换后的四个顶点transformed_square = square @ matrix.T# 绘制原始单位正方形ax.plot(square[:, 0], square[:, 1], 'bo-', label='Original Square')# 绘制变换后的平行四边形ax.plot(transformed_square[:, 0], transformed_square[:, 1], 'ro-', label='Transformed Parallelogram')# 设置标题和图例ax.set_title(title)ax.axhline(0, color='grey', lw=1)ax.axvline(0, color='grey', lw=1)ax.grid(True)ax.legend()ax.set_aspect('equal')# 定义矩阵 A
A = np.array([[2, 1], [1, 2]])# 计算行列式
det_A = np.linalg.det(A)# 创建绘图
fig, ax = plt.subplots(figsize=(8, 8))
plot_transformation(A, ax, f"Transformation by Matrix A (det = {det_A:.2f})")
plt.show()

结果分析

1. 原始单位正方形：由蓝色线条表示，四个顶点为 $(0,0)$, $(1,0)$, $(1,1)$, $(0,1)$。
2. 变换后的平行四边形：由红色线条表示，是单位正方形通过矩阵 A 变换后的结果。
3. 行列式的值：通过计算 det_A = np.linalg.det(A) 得到的行列式为 3.0。

解释

行列式的值为 3.0，表示变换后的平行四边形的面积是原始单位正方形面积的3倍。也就是说，通过矩阵 A 变换后，单位正方形的面积增加了3倍，说明这个变换的面积缩放因子是3。

Determinant（行列式）是一个对于方阵的特定函数，其形式定义如下：

给定一个 $n\times n$ 的方阵 $A$，其行列式 $\det (A)$ 可以通过递归的方式定义如下：

1. 对于 $1\times 1$ 矩阵：$\det ([a])=a$其中 $a$ 是矩阵的唯一元素。
2. 对于 $n\times n$ 矩阵 $A$ （其中 $n>1$ ）：$\det (A)={\sum }_{j=1}^n(-1{)}^{1+j}{a}_{1j}\det (A_{1j})$其中 $a_{1j}$ 是矩阵 $A$ 的第1行第 $j$ 列的元素，$A_{1j}$ 是通过删除矩阵 $A$ 的第1行和第 $j$ 列得到的 $(n-1)\times (n-1)$ 子矩阵。
   这个递归定义称为Laplace 展开或余子式展开。它将计算一个大矩阵的行列式转化为计算它的子矩阵的行列式，直到计算到 $1\times 1$ 矩阵为止。

性质和重要性

行列式具有许多重要的性质：

• 矩阵可逆性：一个 $n\times n$ 矩阵 $A$ 可逆当且仅当 $\det (A)\ne 0$。
• 体积和方向：行列式的绝对值表示由矩阵的列向量构成的几何体（如平行四边形、平行六面体）的有向体积，而行列式的符号表示空间变换的方向性。
• 特征值的乘积：矩阵的行列式等于其特征值的乘积。
• 矩阵乘法：对于两个 $n\times n$ 矩阵 $A$ 和 $B$，有 $\det (AB)=\det (A)\det (B)$。
  行列式在线性代数、微分几何、概率论等数学领域中具有广泛的应用，是理解和分析矩阵和线性变换性质的关键工具之一。

行列式的意义和应用

行列式的定义

对于 $n\times n$ 矩阵 $A$，其行列式定义如下：

• 2x2矩阵：$\det (A)=\left|\begin{array}{cc}a& b\\ c& d\end{array}\right|=ad-bc$
• 3x3矩阵：$\det (A)=\left|\begin{array}{ccc}a& b& c\\ d& e& f\\ g& h& i\end{array}\right|=a(ei-fh)-b(di-fg)+c(dh-eg)$

$$\det (A)=a_{11}\left|\begin{array}{cc}{a}_{22}& a_{23}\\ a_{32}& a_{33}\end{array}\right|-a_{12}\left|\begin{array}{cc}{a}_{21}& a_{23}\\ a_{31}& a_{33}\end{array}\right|+a_{13}\left|\begin{array}{cc}{a}_{21}& a_{22}\\ a_{31}& a_{32}\end{array}\right|$$

• 一般 $n\times n$ 矩阵：
  行列式的计算可以通过递归展开（Laplace展开）来完成。对于任意 $n\times n$ 矩阵 $A$，其行列式定义为：$\det (A)={\sum }_{j=1}^n(-1{)}^{1+j}{a}_{1j}\det (A_{1j})$其中 $A_{1j}$ 是通过删除矩阵 $A$ 的第1行和第 $j$ 列得到的子矩阵。

行列式的一些主要意义：

1. 几何意义

• 有向体积：在二维空间中，行列式的绝对值表示由矩阵列向量形成的平行四边形的面积；在三维空间中，它表示由列向量形成的平行六面体的体积。行列式的符号表示有向体积，即空间变换的方向。
• 线性变换的缩放因子：一个矩阵的行列式表示了该矩阵作为线性变换的缩放因子。正的行列式表示变换保持方向，负的行列式表示变换翻转方向。

2. 代数意义

• 可逆性判断：行列式是判断方阵是否可逆的重要工具。如果一个矩阵的行列式为零，则该矩阵是奇异的，不可逆；如果行列式不为零，则矩阵是可逆的。
• 解线性方程组：行列式在求解线性方程组中起重要作用。通过克拉默法则，行列式可以用于求解方程组的解。

3. 特征值与特征向量、矩阵可逆性

• 特征值的积：一个矩阵的行列式等于其特征值的积。这一性质在矩阵对角化和特征值分析中非常重要。
• -矩阵可逆性：行列式是判断矩阵是否可逆的重要工具。如果一个矩阵的行列式为零，则该矩阵不可逆；如果行列式不为零，则矩阵可逆。

4. 面积和体积计算

• 面积与体积公式：在几何中，行列式用于计算多边形、多面体的面积和体积。例如，三角形的面积可以通过其顶点坐标构成的矩阵行列式计算出来。

通过2D和3D图形展示行列式对应的有向体积

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection# 2D行列式的几何意义
def plot_2d_determinant(matrix):fig, ax = plt.subplots()origin = np.array([[0, 0], [0, 0]])ax.quiver(*origin, matrix[0], matrix[1], color=['r', 'b'], scale=1, scale_units='xy')ax.fill([0, matrix[0, 0], matrix[0, 0] + matrix[0, 1], matrix[0, 1]],[0, matrix[1, 0], matrix[1, 0] + matrix[1, 1], matrix[1, 1]],color='gray', alpha=0.3)ax.set_xlim(-1, 5)ax.set_ylim(-1, 5)ax.set_aspect('equal')plt.grid()plt.title(f"2D Determinant (Area): {np.linalg.det(matrix):.2f}")plt.show()matrix_2d = np.array([[2, 1], [1, 3]])
plot_2d_determinant(matrix_2d)# 3D行列式的几何意义
def plot_3d_determinant(matrix):fig = plt.figure()ax = fig.add_subplot(111, projection='3d')origin = np.zeros((3, 1))ax.quiver(*origin, *matrix[:, 0], color='r')ax.quiver(*origin, *matrix[:, 1], color='g')ax.quiver(*origin, *matrix[:, 2], color='b')v = np.array([[0, 0, 0], matrix[:, 0], matrix[:, 1], matrix[:, 0] + matrix[:, 1], matrix[:, 2], matrix[:, 0] + matrix[:, 2], matrix[:, 1] + matrix[:, 2], matrix[:, 0] + matrix[:, 1] + matrix[:, 2]])verts = [[v[0], v[1], v[3], v[2]], [v[0], v[1], v[5], v[4]], [v[1], v[3], v[7], v[5]],[v[0], v[2], v[6], v[4]], [v[2], v[3], v[7], v[6]], [v[4], v[5], v[7], v[6]]]ax.add_collection3d(Poly3DCollection(verts, alpha=.25, linewidths=1, edgecolors='r'))ax.set_xlim([0, 5])ax.set_ylim([0, 5])ax.set_zlim([0, 5])plt.title(f"3D Determinant (Volume): {np.linalg.det(matrix):.2f}")plt.show()matrix_3d = np.array([[2, 1, 1], [1, 2, 1], [1, 1, 2]])
plot_3d_determinant(matrix_3d)

在二维空间中，行列式的绝对值表示由矩阵列向量形成的平行四边形的面积；在三维空间中，它表示由列向量形成的平行六面体的体积。

通过递归展开法计算行列式

import numpy as npdef determinant_recursive(matrix):"""通过递归计算矩阵的行列式"""if matrix.shape[0] == 1:return matrix[0, 0]elif matrix.shape[0] == 2:return matrix[0, 0] * matrix[1, 1] - matrix[0, 1] * matrix[1, 0]else:det = 0for col in range(matrix.shape[1]):sub_matrix = np.delete(np.delete(matrix, 0, axis=0), col, axis=1)cofactor = ((-1) ** col) * matrix[0, col] * determinant_recursive(sub_matrix)det += cofactorreturn det# 测试递归计算行列式
matrix_3d = np.array([[2, 1, 1], [1, 2, 1], [1, 1, 2]])
det_value_recursive = determinant_recursive(matrix_3d)
det_value_np = np.linalg.det(matrix_3d)print(f"Determinant of the matrix (recursive): {det_value_recursive:.2f}")
print(f"Determinant of the matrix (np.linalg.det): {det_value_np:.2f}")

行列式的正负

当行列式为正时，变换后的图形保持了原来的方向（没有镜像反转），单位向量的顺序保持不变。
当行列式为负时，变换后的图形发生了镜像反转，单位向量的顺序被颠倒。

import numpy as np
import matplotlib.pyplot as pltdef plot_linear_transformation(matrix, color, label):origin = np.array([[0, 0], [0, 0]])  # 原点unit_vectors = np.array([[1, 0], [0, 1]])  # 单位向量# 变换后的向量transformed_vectors = matrix @ unit_vectors.T# 绘制变换后的向量plt.quiver(*origin, transformed_vectors[0, :], transformed_vectors[1, :], color=color, alpha=0.5, scale=1, scale_units='xy')# 绘制变换后的单位正方形square = np.array([[0, 1, 1, 0, 0], [0, 0, 1, 1, 0]])  # 单位正方形transformed_square = matrix @ squareplt.plot(transformed_square[0, :], transformed_square[1, :], color=color, label=label)# 创建绘图
plt.figure()# 正的行列式
matrix_positive_det = np.array([[1, 2], [0, 1]])
plot_linear_transformation(matrix_positive_det, 'blue', f"Positive Determinant: {np.linalg.det(matrix_positive_det):.2f}")
print(np.linalg.det(matrix_positive_det))# 负的行列式
matrix_negative_det = np.array([[0, 1], [1, 0]])
plot_linear_transformation(matrix_negative_det, 'red', f"Negative Determinant: {np.linalg.det(matrix_negative_det):.2f}")
print(np.linalg.det(matrix_negative_det))# 原始单位向量
origin = np.array([[0, 0], [0, 0]])  # 原点
unit_vectors = np.array([[1, 0], [0, 1]])  # 单位向量
plt.quiver(*origin, unit_vectors[:, 0], unit_vectors[:, 1], color=['black', 'black'], scale=1, scale_units='xy')
plt.plot([0, 1, 1, 0, 0], [0, 0, 1, 1, 0], 'black', linestyle='--', label='Original Square')plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.gca().set_aspect('equal', adjustable='box')
plt.grid(True)
plt.legend()
plt.title("Comparison of Positive and Negative Determinants")
plt.show()

正的行列式（保持方向和缩放）：

变换矩阵：[[1, 2], [0, 1]]
单位向量 (1, 0) 和 (0, 1) 分别变换为 (1, 0) 和 (2, 1)。
绘制结果：单位正方形在变换后依然是一个平行四边形，且单位向量的顺序（红色到蓝色）保持不变，表示变换没有翻转方向。
负的行列式（翻转方向和缩放）：

变换矩阵：[[0, 1], [1, 0]]
单位向量 (1, 0) 和 (0, 1) 分别变换为 (0, 1) 和 (1, 0)。
绘制结果：单位正方形在变换后依然是一个平行四边形，但单位向量的顺序（红色到蓝色）被颠倒，表示变换翻转了方向。
通过这些图形，我们可以直观地看到：

当行列式为正时，变换后的图形保持了原来的方向（没有镜像反转），单位向量的顺序保持不变。
当行列式为负时，变换后的图形发生了镜像反转，单位向量的顺序被颠倒

行列式计算转化为更小的子矩阵的行列式计算

import numpy as np
import matplotlib.pyplot as plt
import networkx as nxdef determinant_recursive_steps(matrix):"""通过递归计算矩阵的行列式，并记录每一步"""steps = []def recursive_determinant(matrix, depth=0):if matrix.shape[0] == 1:return matrix[0, 0]elif matrix.shape[0] == 2:result = matrix[0, 0] * matrix[1, 1] - matrix[0, 1] * matrix[1, 0]steps.append((matrix.tolist(), result, depth))return resultelse:det = 0for col in range(matrix.shape[1]):sub_matrix = np.delete(np.delete(matrix, 0, axis=0), col, axis=1)cofactor = recursive_determinant(sub_matrix, depth + 1)cofactor = ((-1) ** col) * matrix[0, col] * cofactordet += cofactorsteps.append((matrix.tolist(), det, depth))return detdeterminant = recursive_determinant(matrix)return determinant, stepsdef plot_determinant_steps(steps):"""使用NetworkX绘制行列式计算的步骤"""G = nx.DiGraph()labels = {}for i, (matrix, value, depth) in enumerate(steps):node_label = f"Step {i+1}:\n{matrix}\nValue: {value:.2f}"G.add_node(i, label=node_label)labels[i] = node_labelif i > 0:G.add_edge(i - 1, i)pos = nx.spring_layout(G)plt.figure(figsize=(12, 8))nx.draw(G, pos, with_labels=True, labels=labels, node_size=3000, node_color="lightblue", font_size=10, font_weight="bold")plt.title("Steps of Determinant Calculation (Laplace Expansion)")plt.show()# 示例矩阵
matrix_3d = np.array([[2, 1, 1], [1, 2, 1], [1, 1, 2]])# 计算行列式并记录步骤
det_value, steps = determinant_recursive_steps(matrix_3d)# 使用numpy的行列式计算函数验证结果
det_value_numpy = np.linalg.det(matrix_3d)# 打印行列式的值
print(f"Determinant of the matrix (recursive): {det_value:.2f}")
print(f"Determinant of the matrix (numpy): {det_value_numpy:.2f}")# 绘制行列式计算的步骤
plot_determinant_steps(steps)