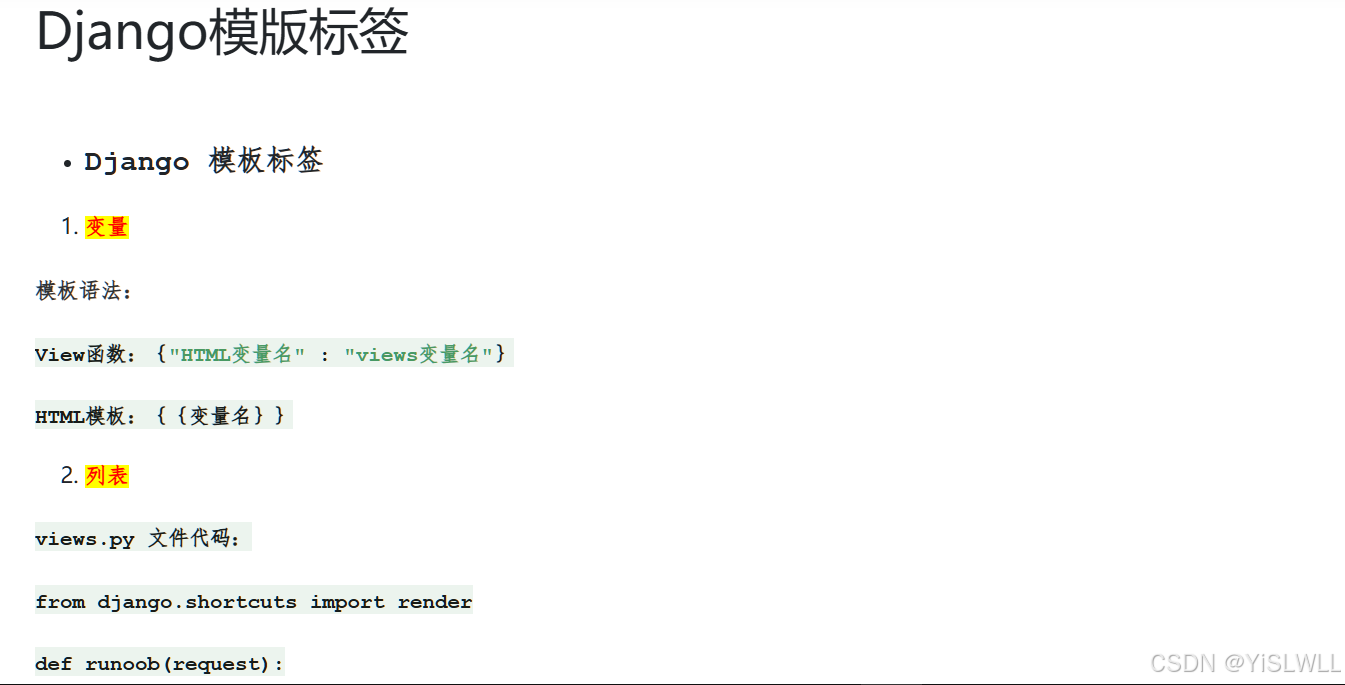
在前端开发中,排序算法是一种非常重要的工具。无论是对数组进行排序以展示数据,还是对复杂对象进行排序以实现特定的功能,理解和掌握常见的排序算法对于提高开发效率和代码质量至关重要。本文将介绍几种前端常见的排序算法。
一、冒泡排序(Bubble Sort)
冒泡排序是一种简单的排序算法。它重复地走访要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
以下是使用 JavaScript 实现冒泡排序的代码:
冒泡排序的时间复杂度为
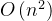
,
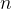
是数组的长度。它的优点是实现简单,容易理解;
缺点是效率较低,不适合处理大规模数据。
二、选择排序(Selection Sort)
选择排序的工作原理是:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
以下是使用 JavaScript 实现选择排序的代码:
选择排序的时间复杂度也为
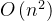
。与冒泡排序相比,选择排序在交换元素的次数上可能会少一些,但总体效率仍然不高。
三、插入排序(Insertion Sort)
插入排序的基本思想是:将一个数据插入到已经排好序的有序数据中,得到一个新的、个数加一的有序数据。
以下是使用 JavaScript 实现插入排序的代码:
插入排序的时间复杂度同样为
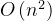
,在某些情况下,它的性能可能会比冒泡排序和选择排序好一些。比如,当数组部分有序时,插入排序的效率会比较高。
四、快速排序(Quick Sort)
快速排序是一种高效的排序算法,它采用分治的思想,将一个数组分成两个子数组,然后对这两个子数组分别进行排序。
以下是使用 JavaScript 实现快速排序的代码:
快速排序的平均时间复杂度为
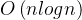
,在处理大规模数据时效率较高。在最坏情况下,它的时间复杂度会退化为
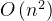
。
五、归并排序(Merge Sort)
归并排序也是一种采用分治思想的排序算法。它将数组分成两个子数组,分别对这两个子数组进行排序,然后将两个有序的子数组合并成一个有序的数组。
以下是使用 JavaScript 实现归并排序的代码:
归并排序的时间复杂度为
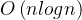
,它的性能比较稳定,不会出现快速排序在最坏情况下的时间复杂度退化问题。
六、堆排序(Heap Sort)
堆排序是利用堆这种数据结构而设计的一种排序算法。堆是一种完全二叉树,它分为大根堆和小根堆。大根堆的每个节点的值都大于或等于其子节点的值,小根堆的每个节点的值都小于或等于其子节点的值。
以下是使用 JavaScript 实现堆排序的代码:
堆排序的时间复杂度为
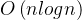
,它的空间复杂度为
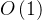
,是一种比较高效的排序算法。
七、计数排序(Counting Sort)
计数排序是一种非比较型整数排序算法。它的核心思想是利用一个额外的数组来统计每个元素出现的次数,然后根据统计结果将元素依次放入正确的位置。
以下是使用 JavaScript 实现计数排序的代码:
计数排序的时间复杂度为
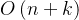
,其中
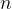
是数组的长度,
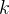
是数组中元素的取值范围。它的优点是速度快,适用于元素取值范围较小的情况;缺点是需要额外的空间来存储计数数组。
八、总结
在前端开发中,选择合适的排序算法可以提高代码的性能和效率。对于小规模数据,冒泡排序、选择排序和插入排序可能是简单而直接的选择;对于大规模数据,快速排序、归并排序、堆排序和计数排序通常是更好的选择。了解这些常见的排序算法的原理和实现方法,可以帮助我们更好地解决各种排序问题,提高前端开发的质量。