多种算法解决组合优化问题平台

🏡作者主页：点击！

🤖编程探索专栏：点击！

⏰️创作时间：2024年11月11日7点12分

点击开启你的论文编程之旅https://www.aspiringcode.com/content?id=17302099790265&uid=ef7618fa204346ff9871cc08fe022561

本文链接

一、背景及意义描述

组合优化问题及相关算法概述

- 组合优化问题在实际中广泛存在，如旅行商问题、背包问题、任务分配问题等，具有决策变量、约束条件和NP难等特性。
- 介绍了多种解决组合优化问题的算法：

- - 遗传算法：20世纪70年代由John Holland提出，依据达尔文生物进化论和门德尔遗传学理论，将初始解映射为“染色体”，经选择、交叉、变异等过程进化为最优解。
  - 贪心算法：总是做出当前最好选择得局部最优解，贪心策略需无后效性。
  - 动态规划算法：将问题分解为子问题，先解子问题再得原问题解，需满足最优化原理、无后效性和重叠性。
  - 分治法：将大问题分割为小问题各个击破，要求问题易解决、可分解、子问题解可合并且相互独立。
  - 回溯法：在解空间树深度优先搜索，不包含解则回溯。
  - 分支限界法：以广度优先或最小耗费优先搜索解空间树，通过舍弃不可行或非最优解的儿子结点提高效率。

研究目的

- 旨在对比分析二进制狼群算法、蝙蝠混合算法、烟花优化算法以及回溯算法、分支限界算法、贪心算法在求解0 - 1背包问题、TSP问题和VRP问题时的性能表现。
- 阐述了各问题特点及不同算法求解策略：

- - 0 - 1背包问题：是NP难问题，贪心算法可能无法得全局最优解，回溯法时间复杂度高，分支限界法可减少搜索时间，二进制狼群算法等通过模拟自然现象或生物行为寻找最优解，可能有更好全局搜索能力和收敛速度。
  - TSP问题：贪心算法易陷局部最优，回溯法时间复杂度高，分支限界法可剪枝但大规模问题可能效率低，烟花优化算法等通过模拟行为寻找最优路径，可能性能更好。
  - VRP问题：二进制狼群算法等通过迭代优化找最优解，回溯算法等处理复杂问题可能效率低。

- 通过对比分析算法在不同问题中的最优值、最差值、方差、用时等指标，了解算法优缺点，为实际应用选合适算法提供参考，还可改进优化算法提高性能。

二、概述

本文介绍了组合优化问题及多种解决算法，旨在对比分析二进制狼群算法、蝙蝠混合算法、烟花优化算法等与回溯、分支限界、贪心算法在0 - 1背包、TSP和VRP问题上的性能，为应用选算法及改进算法提供参考。原文参考链接：
混合贪婪烟花算法
二进制狼群算法
混合蝙蝠算法

三、问题描述与研究目的

题目描述

- 0 - 1背包问题：在给定背包容量和物品的重量、价值情况下，每个物品只能选一次，目标是使背包中物品总价值最大。
- TSP问题：给定城市和城市间距离，旅行商要找到访问每座城市仅一次并返回起始城市的最短回路。
- VRP问题：涉及优化配送或服务路径，在满足车辆容量、顾客需求、配送时间窗等条件下，选择最佳路线以最小化配送成本或路径长度。

研究目的：对比分析二进制狼群算法、蝙蝠混合算法、烟花优化算法、回溯算法、分支限界算法和贪心算法在上述三个问题中的性能表现，为实际应用提供参考，并通过实验结果改进算法。

四、理论基础

回溯算法原理

问题求解方式

- 回溯算法是一种通用的搜索算法，它通过系统地探索问题的所有可能解空间来找到满足特定条件的解。它从问题的某个初始状态开始，按照一定的规则逐步生成可能的解，并在每一步检查当前生成的部分解是否满足问题的约束条件。如果满足，则继续扩展这个部分解；如果不满足，则回溯到上一步，尝试其他可能的选择。这个过程不断重复，直到找到一个完整的解或者确定问题无解。

最小重量机器设计问题示例

- 问题描述：假设有不同类型的机器部件可供选择，每个部件都有其特定的重量和性能参数。目标是选择一组部件，使得组装后的机器满足特定的性能要求，同时总重量最小。
- 解空间树构建：

- - 将每个部件作为一个节点，从根节点开始，每次选择一个部件进行扩展。
  - 如果一个节点代表的部件组合不满足约束条件（如性能要求未满足或总重量超过限制），就不再继续扩展该节点的子树。
  - 在搜索过程中，采用深度优先搜索策略，从根节点出发，逐步探索解空间树的各个分支。如果发现某个节点的部件组合已经超过了重量限制，就回溯到上一个节点，尝试其他部件。根据搜索要求，回溯算法在解问题的所有解时，必须回溯到根节点，且根节点的所有子树都被搜索后才结束；解问题的一个解时，只要搜索到问题的一个解就可结束。

贪心算法原理

基本策略

- 贪心算法在对问题求解时，总是基于当前的局部信息做出看起来是最优的选择，而不考虑这个选择对未来可能产生的影响。它的核心思想是通过一系列局部最优的决策来尝试达到全局最优解，但这种方法并不一定能保证得到全局最优解，因为它没有考虑到问题的整体结构和所有可能的情况。

超市找零问题示例

- 策略选择：假设需要找零的金额为一定值，超市有不同面额的纸币和硬币可供选择。贪心算法的策略可能是优先选择面额较大的货币进行找零。例如，如果要找零10元，超市有5元、2元、1元的纸币和硬币，贪心算法会首先选择5元纸币，然后再考虑2元纸币等。这样可以尽快减少剩余找零金额。然而，这种策略并不一定能得到全局最优解。例如，如果只有一张5元纸币，而有大量的2元纸币，且需要找零的金额为8元，按照贪心算法选择5元纸币后，剩下3元需要用2元纸币找零，可能会导致无法找到最优的找零方案（可能更优的方案是使用4张2元纸币）。

分支限界算法原理

搜索策略

- 分支限界法是一种用于求解最优化问题的算法，它基于对解空间树的搜索来找到最优解。它采用广度优先搜索策略或者按照某种优先级（通过估算目标函数可能取值）对解空间树中的节点进行搜索。在搜索过程中，它会对每个节点进行评估，根据评估结果决定是否进一步扩展该节点以及确定扩展的顺序。

解空间组织方法

- 队列式分支限界法：按照队列先进先出（FIFO）原则选取下一个结点为扩展结点。在解决问题时，将初始状态加入队列，每次从队列中取出一个节点进行扩展，将新生成的节点按照一定规则加入队列。这样可以保证在搜索过程中，先处理较早生成的节点，逐步向更深入的解空间探索。
- 优先队列式分支限界法：按照优先队列中规定的优先级选取优先级最高的结点成为当前扩展结点。优先级可以根据问题的特点进行定义。例如，在求解0 - 1背包问题时，可以将节点对应的背包价值作为优先级，优先处理价值较高的节点。这样可以更快地找到有潜力的解，提高搜索效率。

设计原理

- 首先要确定问题的解空间树结构，这需要根据问题的特点进行分析和构建。例如，在解决0 - 1背包问题时，可以将每个物品的选择作为一个分支，构建一棵二叉树表示所有可能的物品选择组合。然后定义限界函数，用于估算当前节点对应解的目标函数值的上下界。在搜索过程中，根据限界函数的值来判断是否继续扩展该节点。如果限界函数值表明该节点不可能导致更优的解，则可以舍弃该节点，从而减少搜索空间。最后，选择合适的解空间组织方式（队列式或优先队列式），根据问题的性质和需求来决定。

烟花算法原理

算法起源与特点

- 烟花优化算法（Firework Algorithm，FWA）是受烟花爆炸产生火星，并继续分裂爆炸这一过程启发而得出的算法。它具有进化能力强、搜索速度快、寻优能力强的特点。该算法于2010年发表在知名SCI期刊Advances in Swarm Intelligence上，目前在谷歌学术上被引率高达1214次。

烟花行为模拟

- 火花数量与适应度关系：每个烟花产生的火花数量与烟花的适应度值相关。适应度值较好的烟花会产生较多的火花，以便在其周围进行更精细的搜索；适应度值较差的烟花则产生较少的火花，避免在不太有希望的区域浪费搜索资源。
- 爆炸幅度与适应度关系：烟花的爆炸幅度也与适应度值有关。适应度值较好的烟花爆炸幅度较小，以便在局部进行更深入的技能搜索；适应度值较差的烟花爆炸幅度较大，以便在更大的范围内进行搜索。
- 保持火花多样性策略：为了保持火花的多样性，算法还采用了一些策略，例如随机选择受影响的维度等。

应用示例

- 在优化问题中，烟花算法可以应用于各种类型的问题，如函数优化、组合优化等。以0 - 1背包问题为例，烟花算法可以将每个可能的物品选择组合看作一个烟花，通过不断地爆炸和产生火花来搜索最优的物品选择方案。在TSP问题中，烟花算法可以将每个可能的路径看作一个烟花，通过爆炸和火花的扩散来寻找最短的旅行路径。

蝙蝠混合算法原理

算法基础

- 蝙蝠混合算法是一种结合了蝙蝠算法和其他算法优点的新型智能优化算法。它模拟了蝙蝠在自然界中的回声定位和觅食行为，通过调节响度和脉冲频率实现局部搜索和全局搜索的平衡。

蝙蝠行为模拟

- 首先初始化一群蝙蝠个体，每个个体代表问题的一个解。然后，通过模拟蝙蝠的回声定位行为，计算每个个体的适应度值，并根据适应度值确定当前最优解。接着，利用蝙蝠的脉冲发射和接收机制，更新个体的位置和速度，实现局部搜索和全局搜索的平衡。在搜索过程中，根据一定的概率对个体进行变异操作，增加算法的多样性，避免陷入局部最优解。

0 - 1背包问题改进策略

- 引入混沌序列初始化：引入混沌序列对蝙蝠个体的初始位置进行初始化，增加算法的多样性，提高搜索效率。
- 结合Powell搜索策略：结合Powell搜索策略，增强算法的局部搜索能力，加快收敛速度。
- 使用变异策略：使用变异策略，如高斯变异或均匀变异，在一定程度上避免算法陷入局部最优解。
- 动态调整参数：动态调整蝙蝠的脉冲频率和响度，根据搜索的进展调整算法的，搜索范围和精度。

二进制狼群算法原理

狼群行为模拟

- 二进制狼群算法模拟了自然界中狼群的捕食行为，主要涉及头狼、探狼和猛狼三种角色的协作。头狼在狼群中处于领导地位，它通常是当前狼群中适应度最高的狼，负责指挥狼群的行动方向。探狼负责在周围环境中探索可能存在猎物的区域，它们会在一定范围内随机地搜索，一旦发现有较好的区域（适应度较好的解所在区域），就会向头狼报告。猛狼当探狼发现有潜在的猎物区域后，会迅速地朝着该区域奔袭，进一步对该区域进行搜索和逼近猎物，它们的行动相对更具攻击性和指向性，以期望快速找到更优的解。

二进制编码相关操作

- 个体编码：每个狼个体（对应优化问题中的一个解）用二进制串来表示。例如，对于一个有n个变量的0 - 1背包问题，一只狼可以表示为一个长度为n的二进制串，串中的每一位对应一个物品是否放入背包（0表示不放入，1表示放入）。
- 位置更新方式：

- - 探狼的探索：探狼在二进制空间中进行探索时，其探索方式是对自身的二进制编码进行随机的位翻转操作来生成新的可能位置（解）。比如，一只探狼的二进制编码为[0, 1, 0, 1]，它可能通过随机选择其中一位（假设选择了第2位）进行翻转，得到新的编码[0, 0, 0, 1]，以此来探索新的区域。
  - 猛狼的奔袭：当探狼发现有较好的区域并报告后，猛狼朝着该区域奔袭的过程中，也是通过对自身二进制编码的调整来实现位置更新。一种常见的做法是，根据与目标区域（由探狼发现的较好位置）的差异程度，有针对性地对某些位进行翻转。例如，如果猛狼的编码为[1, 0, 1, 0]，目标区域编码为[1, 1, 0, 0]，猛狼可能会分析出与目标区域在第2位和第4位有差异，然后根据一定的概率决定是否对这两位进行翻转，以更接近目标区域（即找到更优解）。
  - 头狼的引领：头狼作为狼群的领导者，其位置更新同样是基于二进制编码的调整。头狼会根据整个狼群的整体情况（如其他狼的位置和适应度等），对自身的二进制编码进行优化。比如，如果发现大部分狼在某些位上的取值比较集中且对应着较好的适应度，头狼可能会考虑将自身相应位的值进行调整，以更好地引领狼群朝着更优解的方向前进。

- 适应度评估：对于二进制狼群算法所处理的问题，需要根据具体问题定义合适的适应度函数。以0 - 1背包问题为例，适应度函数可能会考虑放入背包物品的总价值、背包的重量限制等因素，通过计算得到每个狼个体（二进制编码表示的解）的适应度值，以此来判断解的优劣程度，进而指导狼群的搜索行为。

五、算法设计

二进制狼群算法设计思路

- 原理介绍：狼群中不同角色分工协作，介绍了位置编码、目标函数值、距离定义、反置操作和运动算子等概念。
- 智能行为和规则：包括游走行为、召唤行为和围攻行为。
- 修复机制：对不满足背包容积限制的人工狼进行修复。
- 算法流程：包括初始化、确定头狼并执行游走行为、猛狼运动、更新围攻人工狼位置、更新头狼和狼群并修复位置编码以及判断终止条件等步骤。
- 代码实现（0 - 1背包问题、TSP问题、VRP问题）：给出了伪代码和实现思路，包括参数设置、狼群初始化、相关函数定义以及主循环中的操作，最后计算结果并绘制曲线返回。

输入：物品数量num_items，背包容量capacity，物品重量列表weights，物品价值列表values
输出：背包能装入物品的最佳价值best_value，最差价值worst_value，所有狼适应度值的方差variance，算法运行时间elapsed_time1. 初始化参数- 设置狼的数量num_wolves，最大迭代次数max_iterations，最大游走次数max_walk_iterations，游走步长walk_step，攻击步长attack_step，距离因子distance_factor，更新因子update_factor
2. 狼群初始化- 使用贪婪算法初始化狼群位置wolves- 初始化适应度字典fitness_dict，用于存储已计算的解决方案的适应度- 记录开始时间start_time
3. 定义函数- calculate_fitness函数：计算解决方案的总价值和总重量，如果已计算过则直接从字典中获取- calculate_distance函数：计算两个解决方案之间的距离
4. 主循环（迭代）- 对于每次迭代iteration（从0到max_iterations - 1）：- 对于每只狼i（从0到num_wolves - 1）：- 计算当前狼的适应度（价值和重量）- 如果当前狼的价值小于最差价值，更新最差价值- 如果当前狼的价值小于最佳价值：- 进行探狼游走操作（随机改变一些位），在最大游走次数内寻找更好的解决方案- 如果当前狼与最佳解决方案的距离小于距离因子：- 根据最佳解决方案更新当前狼的位置- 根据更新因子更新狼群位置- 每10次迭代：- 对每只狼尝试随机生成新的解决方案，如果更好则替换- 找到当前狼群中最佳的狼，如果比全局最佳更好，则更新全局最佳解决方案及相关值，并记录最佳和最差适应度历史
5. 计算结果- 计算所有狼的适应度值- 记录结束时间end_time，计算运行时间elapsed_time- 计算所有狼适应度值的方差variance
6. 绘制曲线并返回结果- 绘制最佳适应度和最差适应度随迭代次数的变化曲线- 返回最佳价值best_value，最差价值worst_value，方差variance，运行时间elapsed_time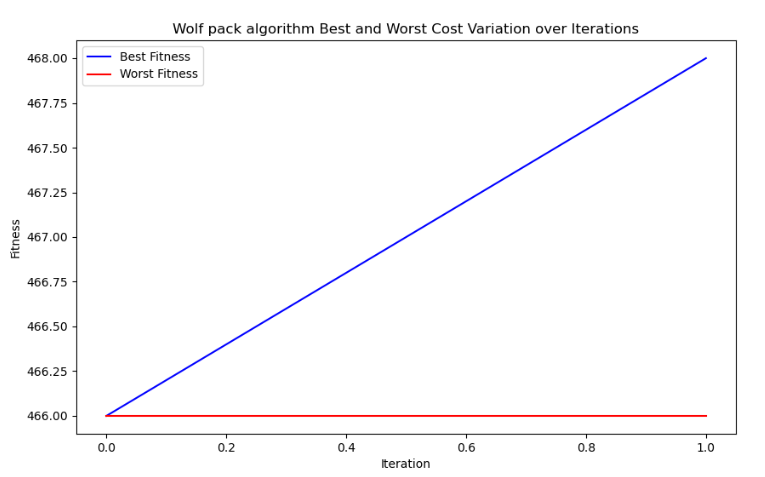

混合蝙蝠算法设计思路

- 原理介绍

- - 初始化蝙蝠位置规则：采用二进制编码随机初始化蝙蝠种群位置。
  - 蝙蝠速度与位置更新规则：重新定义速度，采用遗传算法交叉机制更新位置。
  - 局部搜索规则：引入反置算子进行局部搜索。
  - 贪心策略：对不可行解和可行解分别采用不同的贪心策略。
  - 蝙蝠音量和脉冲发生率更新规则：给出了音量和脉冲发生率的更新公式。

- 设计步骤：包括初始化蝙蝠种群、蝙蝠速度和位置更新、局部搜索、更新满意解、更新音量和脉冲发生率、排列蝙蝠并找到当前最优蝙蝠以及判断迭代次数等步骤。
- **代码实现

输入：背包问题实例problem，蝙蝠数量n_bats，迭代次数n_iterations，参数alpha，gamma
输出：最佳蝙蝠best_bat，最佳价值best_fitness，最佳适应度历史best_fitness_history，最差适应度历史worst_fitness_history1. 初始化参数和蝙蝠种群- 获取物品数量n_items- 随机初始化蝙蝠种群bats- 通过贪心算法获取初始最佳蝙蝠best_bat和最佳价值best_fitness- 初始化最佳和最差适应度历史列表
2. 主循环（迭代）- 对于每次迭代t（从0到n_iterations - 1）：- 对于每只蝙蝠i（从0到n_bats - 1）：- 复制当前蝙蝠new_bat- 根据概率alpha对new_bat的每个元素进行随机翻转- 计算new_bat的适应度（价值和重量）- 如果重量满足背包容量且价值大于最佳价值，则更新最佳蝙蝠和最佳价值- 更新当前蝙蝠为new_bat- 计算当前迭代的最佳和最差适应度值，并添加到相应历史列表
3. 返回结果- 返回最佳蝙蝠best_bat，最佳价值best_fitness，最佳和最差适应度历史列表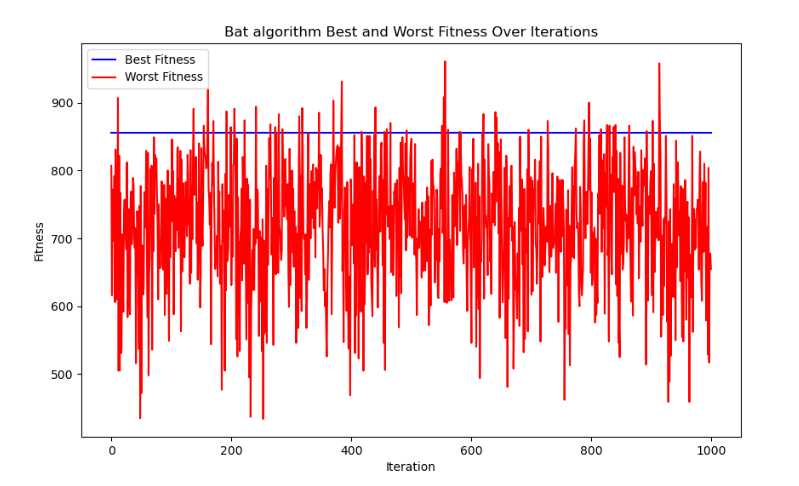

混合贪婪烟花算法设计思路

- 算法设计

- - 爆炸数目和爆炸半径：给出了烟花产生的火花数目和爆炸半径的计算公式，并对火花数量进行限制。
  - 高斯变异与映射规则：选取部分烟花进行高斯变异，并介绍了将变异后的烟花映射到可行域的规则。
  - 模拟退火操作：引入模拟退火机制提高全局搜索能力。
  - 贪心修复算子和贪心优化算子：对选入背包的物品进行修复和修正中间解。

- 代码实现（0 - 1背包问题、TSP问题、VRP问题）：给出伪代码，包括参数和种群初始化、相关函数定义、主循环操作以及结果返回。

回溯算法设计思路

- 算法设计：通过深度优先搜索遍历所有可能解来解决0 - 1背包问题。
- 代码实现（0 - 1背包问题、TSP问题、VRP问题）：给出伪代码，包括全局变量初始化、核心递归函数和对外接口函数的定义以及结果返回。

分支限界算法设计思路

- 算法设计：在解空间树上搜索，利用优先队列根据节点上界价值排序，优先扩展上界价值较大的节点。
- 代码实现（0 - 1背包问题、TSP问题、VRP问题）：给出伪代码，包括初始化、相关类和函数定义、核心循环操作以及结果返回。

贪心算法设计思路

- 算法设计：通过贪心算法和局部搜索，并尝试不同贪心策略找到较优解。
- **代码实现

输入：物品维度dimension，物品重量列表weights，物品价值列表values，背包容量capacity
输出：背包能装入物品的最佳价值best_fitness，最差价值worst_fitness，所有解适应度值的方差variance，算法运行时间elapsed_time1. 初始化参数和种群- 设置种群大小population_size，最大迭代次数max_iterations，初始温度initial_temperature，上下界lower_bound和upper_bound，高斯变异标准差sigma- 使用Tent映射初始化种群population- 初始化最佳解best_solution为None，最佳价值best_fitness为负无穷，最差价值worst_fitness为正无穷，适应度值列表fitness_values，最佳和最差价值随时间变化的列表- 记录开始时间start_time
2. 定义函数- tent_map函数：使用Tent映射生成种群- gaussian_mutation函数：对烟花进行高斯变异- mapping_rule函数：将变异后的烟花映射到上下界范围内- simulated_annealing_acceptance函数：根据模拟退火准则判断是否接受新解- greedy_repair函数：对解进行贪心修复- calculate_fitness函数：计算解的适应度- local_search函数：对解进行局部搜索
3. 主循环（迭代）- 对于每次迭代iteration（从0到max_iterations - 1）：- 对于每个个体i（从0到population_size - 1）：- 对个体进行高斯变异、映射规则处理、贪心修复和局部搜索，得到处理后的个体repaired_firework- 计算repaired_firework的适应度fitness- 如果fitness大于最佳价值，更新最佳价值和最佳解- 如果fitness小于最差价值，更新最差价值- 将fitness添加到适应度值列表- 根据模拟退火接受准则决定是否将repaired_firework加入新种群- 更新种群为新种群- 降低温度- 将当前最佳和最差价值添加到相应随时间变化的列表
4. 计算结果- 计算所有解适应度值的平均mean_fitness和方差variance- 记录结束时间end_time，计算运行时间elapsed_time
5. 绘制曲线并返回结果- 绘制最佳和最差价值随迭代次数的变化曲线- 返回最佳价值best_fitness，最差价值worst_fitness，方差variance，运行时间elapsed_time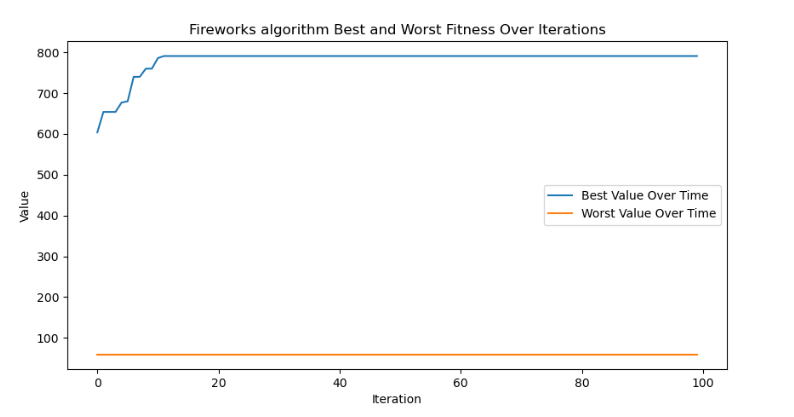

四、可视化界面设计

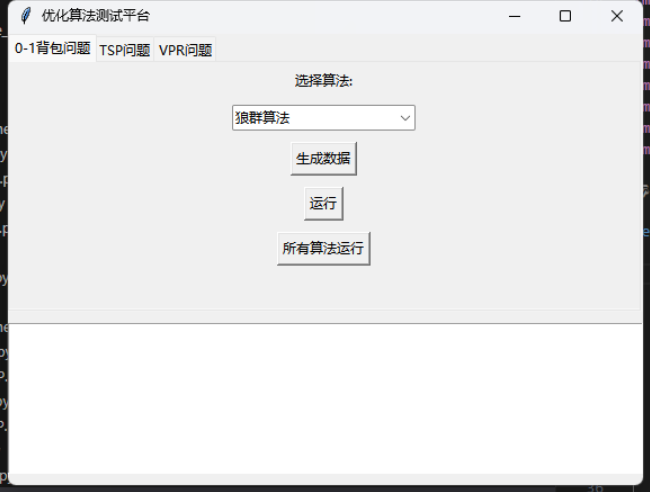
界面功能展示：实现了一个优化算法测试平台，用于测试不同类型组合优化问题的多种算法。用户可选择问题类型、算法，生成随机数据并运行算法获取结果展示在界面上。
代码实现

- 主程序：导入必要库和模块，定义全局变量和数据存储结构，创建主窗口及界面布局，启动主窗口事件循环。
- 数据生成相关函数：分别针对0 - 1背包问题、TSP问题和VRP问题设置参数取值范围并随机生成相应数据。
- 算法运行相关函数：根据算法名称和问题参数调用相应算法函数并返回结果。
- 界面交互相关函数：包括生成数据函数、运行单个算法按钮点击函数和运行所有算法按钮点击函数，分别实现数据生成、单个算法运行和所有算法运行的功能。

六、总结和展望

研究结论总结

- 性能表现方面：贪心算法速度快但通常是局部最优解；回溯算法能找到全局最优解但时间复杂度高；分支限界法提高了搜索效率但大规模问题仍可能耗时；二进制狼群算法、蝙蝠混合算法和烟花优化算法具有较好的全局搜索能力和收敛速度。在不同问题中各算法表现各有优劣。
- 可视化界面设计方面：采用随机数据生成方法，通过算法选择和结果指标曲线展示等功能，方便用户观察和比较算法性能。