凸优化理论
研究凸优化之前我们不妨提出几个小问题:
- 什么是优化问题?
- 优化问题的解是什么?
- 什么是凸优化问题?
- 凸优化问题的解决方案是什么?
1.1 优化问题
理解优化问题其实很简单,我们其实从高中事情就一直在做,优化问题的定义是:在一定约束条件下,寻找一个或一组最优解使得某个目标函数达到最大或最小的问题。如果没有约束条件就可以理解为求解函数的最大最小值问题,如果有约束条件我们也接触过,比如在高等数学多元微分中求解条件最值。
求解优化问题一般有两种方案:第一种是数学分析法,如一元函数的优化问题,可以使用导数为零的方法找到极值点,另一种是数值优化方法,通过迭代地改进决策变量的值,逐步逼近最优解,而我们学习过的梯度下降算法就属于数值优化方法。
优化问题的解一般是标量或者一个向量,比如说一元求导的结果往往会得到一个X的值,在X处取到函数的最大最小值。而对于基于样本进行对模型进行迭代优化的问题,优化问题的解往往是一个参数向量。
1.2 凸优化问题
我们直接给出凸优化问题的定义:
设f: R n R^ {n} Rn → \rightarrow →R为目标函数,C ⊆ \subseteq ⊆ R n R^ {n} Rn 为可行域。如果满足以下条件, 则该优化问题为凸优化问题:
1.目标函数f是凸函数,即对于任意x,y ∈ \in ∈ R n R^ {n} Rn 以及任意0 ⩽ \leqslant ⩽ λ \lambda λ ⩽ \leqslant ⩽ 1,都有
f ( λ x + ( 1 − λ ) y ) ⩽ λ f ( x ) + ( 1 − λ ) f ( y ) 。 f(\lambda x+(1- \lambda )y) \leqslant \lambda f(x)+(1- \lambda )f(y)。 f(λx+(1−λ)y)⩽λf(x)+(1−λ)f(y)。
2.可行域C是凸集,即对于任意x,y ∈ \in ∈ C以及任意0 ⩽ \leqslant ⩽ λ \lambda λ ⩽ \leqslant ⩽ 1,都有 λ \lambda λ x+(1- λ \lambda λ )y ∈ \in ∈C。
那么凸优化问题可以表述为:
min x ∈ C f ( x ) 。 \min_{x \in C} f(x)。 x∈Cminf(x)。
其中,求解的目标是在可行域C中找到一个点 $ x^ {*} $ ,使得目标函数f(x)取得最小值,并且满足凸函数和凸集的条件
从几何的角度可以这样去理解凸函数,首先凸函数不要求连续和可导,其次凸函数可以理解为在图像中任取两点连线,如果函数图像在这个连线的下方,则为凸函数:
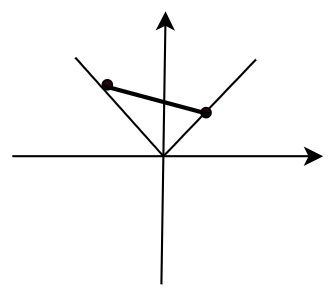
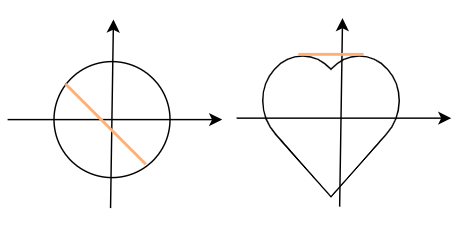
从几何角度也可以这样去理解凸集,在集合范围内任取两点连线,如果两个点的连线仍然在集合内,那么该集合为凸集,显然如果集合是一个圆或者椭圆则为凸集,如果集合是一个心形则是非凸集。
1.3 凸优化问题的分类
凸优化问题可以根据目标函数和约束条件划分为:
- 凸线性规划问题:目标函数是线性的,约束条件是仿射
- 凸二次规划问题:目标函数是二次函数,约束条件是仿射
- 凸半定规划问题:目标函数和约束条件涉及半正定矩阵
1.4 凸二次规划通过拉格朗日对偶法转最小最大问题
问题的一般形式:设初始优化问题为P,则P为
min f ( x ) s . t . C i ( x ) ≤ 0 , i = 1 , 2 , . . . k H j ( x ) = 0 , j = 1 , 2 , . . . l \min f(x) \\ s.t. \\ C_i(x)\leq 0,i=1,2,...k\\ H_j(x) =0,j=1,2,...l minf(x)s.t.Ci(x)≤0,i=1,2,...kHj(x)=0,j=1,2,...l
其中目标函数为f(x),优化变量为x,可行域为凸集,约束条件规定x的范围
Step1: 构造拉格朗日函数
L ( x , α , β ) = f ( x ) + ∑ i = 1 k α i C i ( x ) + ∑ j = 1 l β j H j ( x ) s . t . α i ≥ 0 L(x,\alpha,\beta)=f(x)+\sum_{i=1}^k \alpha_iC_i(x)+\sum_{j=1}^l \beta_j H_j(x)\\ s.t.\\ \alpha_i \geq 0 L(x,α,β)=f(x)+i=1∑kαiCi(x)+j=1∑lβjHj(x)s.t.αi≥0
Step2:转换优化问题,则初始问题P可以转化为极小极大拉格朗日函数问题:
p = min x max α , β L ( x , α , β ) p = \min_x \max_{\alpha,\beta} L(x,\alpha,\beta) p=xminα,βmaxL(x,α,β)
Step3.将原问题转为对偶问题
p ∗ = max α , β min x L ( x , α , β ) p^* = \max_{\alpha,\beta} \min_x L(x,\alpha,\beta) p∗=α,βmaxxminL(x,α,β)
Step4.求解出x与 α , β \alpha,\beta α,β的关系,代入L,对 α , β \alpha,\beta α,β极大化求解
那么为什么原问题P能转换为极小极大拉格朗日函数问题呢?我们可以来仔细分析一下:
∵ i f α i ≥ 0 ∵ C i ( x ) ≤ 0 若取 max α i C i ( x ) ∴ α i = 0 o r C i ( x ) = 0 ∵ H j ( x ) = 0 ∴ β j H j ( x ) = 0 ∴ p = min x { f ( x ) , H j ( x ) = 0 , C i ( x ) ≤ 0 ∞ , o t h e r \because if \quad\alpha_i\geq 0 \\ \because C_i(x)\leq 0 \quad 若取\max{\alpha_iC_i(x)} \\ \therefore \alpha_i =0 \quad or \quad C_i(x)=0 \\ \because H_j(x) =0 \\ \therefore \beta_j H_j(x)=0 \\ \therefore p= \min_x \begin{cases} f(x), & H_j(x)=0, C_i(x)\leq 0\\ \infty, & other \end{cases} ∵ifαi≥0∵Ci(x)≤0若取maxαiCi(x)∴αi=0orCi(x)=0∵Hj(x)=0∴βjHj(x)=0∴p=xmin{f(x),∞,Hj(x)=0,Ci(x)≤0other
1.5 极小极大的对偶问题
什么是对偶问题呢?我们直接给出形式再进行分析,以上面的极大极小问题为例?
p = min x max α , β L ( x , α , β ) p = \min_x \max_{\alpha,\beta} L(x,\alpha,\beta) p=xminα,βmaxL(x,α,β)
它的对偶问题是:
p ∗ = max α , β min x L ( x , α , β ) p^* = \max_{\alpha,\beta} \min_x L(x,\alpha,\beta) p∗=α,βmaxxminL(x,α,β)
这样的好处在于,当我们求解时可以先对x进行求解,将 α , β \alpha,\beta α,β看作参数,这样会一定程度上降低我们求解的麻烦,其次求原问题min的时候x是已经被约束的,所以要考虑x的可行域,但是我们在求对偶问题的时候,因为先对x进行最小化求解,所以这个时候x是没有被约束,也就是x的可行域属于R。
为什么会这样呢?我们可以通过放缩直观的分析到:
p ∗ ≤ max α , β min x ∈ 可行域 L ( x , α , β ) p^* \leq \max_{\alpha,\beta} \min_{x \in 可行域}L(x,\alpha,\beta) p∗≤α,βmaxx∈可行域minL(x,α,β)
由于 p ∗ p^* p∗中x取的是全局最小,而现在缩小x的范围,因而能得到 p ∗ p^* p∗要更小一些
同时:
max α , β min x ∈ 可行域 L ( x , α , β ) ≤ min x ∈ 可行域 f ( x ) \max_{\alpha,\beta} \min_{x \in 可行域}L(x,\alpha,\beta) \leq \min_{x \in 可行域} f(x) α,βmaxx∈可行域minL(x,α,β)≤x∈可行域minf(x)
当x属于可行域范围内时,会使得 ∑ j = 1 l β j H j ( x ) \sum_{j=1}^l \beta_j H_j(x) ∑j=1lβjHj(x)这一项为0,使得 ∑ i = 1 k α i C i ( x ) ≤ 0 \sum_{i=1}^k \alpha_iC_i(x) \leq 0 ∑i=1kαiCi(x)≤0,从而拉格朗如函数肯定是小于f(x)的。
最终我们得到:
p ∗ ≤ max α , β min x ∈ 可行域 L ( x , α , β ) ≤ min x ∈ 可行域 f ( x ) p^* \leq \max_{\alpha,\beta} \min_{x \in 可行域}L(x,\alpha,\beta) \leq \min_{x \in 可行域} f(x) p∗≤α,βmaxx∈可行域minL(x,α,β)≤x∈可行域minf(x)
也就是说对偶问题极小值为我们的原始问题提供了一个极小值的下界。当然这个等式并不是最优的,我们十分渴望知道什么时候可以取等号。在解决这个问题之前我们应该先解决一个小问题?
所有的问题都可以采用对偶问题吗?原来的极小极大问题什么时候可以通过取对偶问题来简化计算?
当原凸优化问题满足Slater条件时该问题可以转为一个强对偶性(对偶问题的解可以和原问题的解取等号,也就是上面等号成立的情况)的凸优化问题。
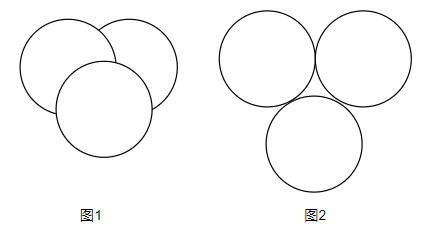
Slater条件:Slater条件是对凸优化问题中不等式约束的限制,我们假设每一个不等式的约束为一个凸集,如果这些凸集相交且有公共交集,则称该问题符合Slater条件,否则则称不符合。如下图,图一为符合slater条件的情况图二则不符合Slater条件,无法转为对偶问题。
接下来我们解决等号的问题,其实我们已经解决了,如果一个凸优化问题同时这个问题符合Slater条件,则代表存在强对偶性,则原问题的解可以等于对偶问题的解。
那么我们又将提出一个问题?是,现在是可以等于对偶问题的解,如此复杂的式子,这个解当然可以根据先求最小再求最大去求,有没有什么简单做法呢?KKT条件
1.6 KKT条件
根据上文,我们直观的了解到,如果一个式子可以转为对偶问题,我们已经能很方便的去对这个问题进行求解,但是强对偶性是一个非常特殊的条件,它的特殊就体现再它又提供给了我们一个方法去求解,也就是KKT条件。KKT条件是解的充分条件,也就是说如果对偶问题具有强对偶性,则该问题的解可以通过KKT条件计算出来,也就是:
{ ∂ x L ( x , α , β ) = 0 α i C i ( x ) = 0 互补松弛条件 C i ( x ) ≤ 0 α i ≥ 0 h j ( x ) = 0 \begin{cases} \partial_x L(x,\alpha,\beta)=0\\ \alpha_iC_i(x) =0 & 互补松弛条件 \\ Ci(x) \leq 0 \\ \alpha_i \geq 0 \\ h_j(x) =0 \end{cases} ⎩ ⎨ ⎧∂xL(x,α,β)=0αiCi(x)=0Ci(x)≤0αi≥0hj(x)=0互补松弛条件
根据KKT条件求出的x为原问题的最优解 α , β \alpha,\beta α,β 为对偶问题的最优解,从这个角度,KKT条件建立了原问题和对偶问题的联系。




![动态规划-背包问题——[模版]01背包(背包母题)](https://i-blog.csdnimg.cn/direct/7b51104ede8c4db092f7232753687ce9.png)













