最后三题，二叉树就结束啦！！！

题目：修剪二叉搜索树

669. 修剪二叉搜索树 - 力扣（LeetCode）

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

示例 1：

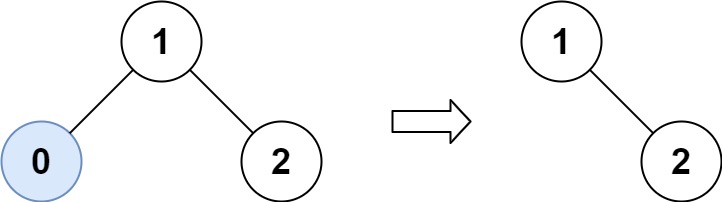
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

 题目分析：

        和上一题的删除二叉树的结点差不多，对树进行遍历，对于不符合的结点直接删除。对于搜索树来说，寻找在范围内的结点也可以利用他的特点。

public class Solution {public TreeNode TrimBST(TreeNode root, int low, int high) {if(root==null) return null;if(root.val<low){//左边一定不符合，直接抛弃TreeNode right=TrimBST(root.right,low,high);return right;}if(root.val>high){TreeNode left=TrimBST(root.left,low,high);return left;}root.left=TrimBST(root.left,low,high);root.right=TrimBST(root.right,low,high);return root;}
}

题目：将有序数组转为二叉搜索树

108. 将有序数组转换为二叉搜索树 - 力扣（LeetCode）

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 平衡二叉搜索树。

题目分析：

        之前以及做过几个类似的题目了，大题的思路都是对数组进行分割，这一题也一样。题目中要求平衡树，事实上，有序数组的中间数就相当于搜索树的中结点。所以每次对数组的范围找中间值，就可以构建树了。

public class Solution {public TreeNode SortedArrayToBST(int[] nums) {return traversal(nums,0,nums.Length-1);}public TreeNode traversal(int[] nums,int left,int right){if(left>right) return null;int mind=left+((right-left)/2);//因为是在原数组的索引，所以需要加leftTreeNode root=new TreeNode(nums[mind]);root.left=traversal(nums,left,mind-1);root.right=traversal(nums,mind+1,right);return root;}
}

 题目：把二叉搜索树转为累加树

538. 把二叉搜索树转换为累加树 - 力扣（LeetCode）

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

 题目分析：

        题目的意思就是将结点的值变成大于等于结点值的所有结点之和。而在搜索树中，大于等于这个结点的范围其实就是结点的右子树范围。

        所以对搜索树进行遍历即可，因为是大于等于，所以我们可以先遍历右子树，并且使用一个值来存结点改变之后的值，方便下一个结点使用。

public class Solution {int pre;//记录前一个结点的值，避免重复累加public TreeNode ConvertBST(TreeNode root) {pre=0;Test(root);return root;}void Test(TreeNode root){if(root==null) return;Test(root.right);//因为是求大于等于，所以先遍历右子树root.val+=pre;pre=root.val;Test(root.left);}
}

对于更详细的解析与其他语言的代码块，可以去代码随想录上查看。

代码随想录 (programmercarl.com)

已刷题目：58