异或和公式

前缀异或和公式

前缀异或和的概念与前缀和类似，但它使用的是异或（XOR）操作而不是加法。异或操作有一些独特的性质，使得前缀异或和在处理某些问题时非常有用。下面是前缀异或和的推导原理：

• 异或操作的性质：

• 前缀异或和的定义：

对于一个数组nums，其前缀异或和数组prefixXor定义为：

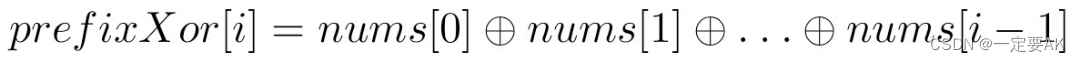
其中，prefixXor[0]通常定义为0，作为基准。

• 计算前缀异或和：

• 初始化：prefixXor[0]=0

• 对于i从 1 到n（数组长度）：

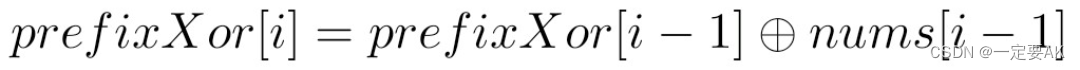
这个递推公式的意思是，当前位置的前缀异或和等于前一个位置的前缀异或和与当前元素的异或。

• 推导过程：

• 假设我们已经有了prefixXor[i-1]，它表示从数组开始到第i-1个元素的异或和。

• 要得到prefixXor[i]，即到第i个元素的异或和，我们只需要将prefixXor[i-1]与第i个元素(nums[i-1]进行异或操作。

• 这是因为异或操作的结合律允许我们将异或操作分组，而不影响最终结果。

• 应用：

• 一旦我们有了前缀异或和数组，我们可以在O(1)时间内计算任意子区间的异或和。

• 对于子区间[l,r]，其异或和可以通过

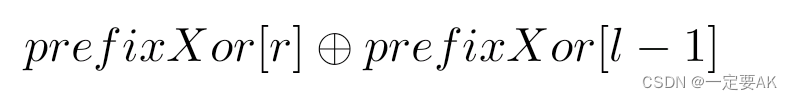
计算得到。这里l和r分别是子区间的起始和结束索引。

子区间的异或和

子区间的异或和可以通过前缀异或和数组来快速计算。这里是一个逐步的推理过程，解释如何得到子区间异或和的公式：

• 前缀异或和数组：首先，我们定义一个前缀异或和数组prefixXor，其中prefixXor[i]表示从数组的开始到第i个元素的连续子数组的异或和。

• 子区间异或和的计算：假设我们想要计算从索引l到索引r（包括l和r）的子区间的异或和。我们可以利用前缀异或和数组来快速得到这个值。

• 利用异或的性质：异或操作有一个重要的性质，即A ^ A = 0和A ^ 0 = A。这意味着，如果我们想要从prefixXor[r]中移除从l-1到0的异或和，我们可以将prefixXor[l-1]异或到prefixXor[r]上。

• 子区间异或和的公式：因此，从l到r的子区间异或和可以通过以下公式计算：

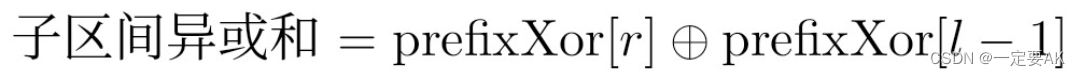
这里，prefixXor[r]包含了从数组开始到r的所有元素的异或和，而prefixXor[l-1]包含了从数组开始到l-1的所有元素的异或和。将这两个值异或，我们就得到了从l到r的子区间的异或和。

• 为什么这样工作：这个公式之所以有效，是因为异或操作的结合律和交换律。结合律允许我们重新组合异或操作，而交换律允许我们改变操作的顺序。通过将prefixXor[r]与prefixXor[l-1]异或，我们实际上是在计算从l到r的所有元素的异或和，同时消除了l-1之前的所有元素的影响。

• 应用：在实际编程中，这个公式允许我们在 O(1)时间内计算任意子区间的异或和，这是非常高效的。这对于解决需要频繁计算子区间异或和的问题非常有用。

通过这种方式，我们可以利用前缀异或和数组来快速计算数组中任意子区间的异或和，这是解决许多与异或和相关的问题的关键技术。

为什么使用异或：

• 异或操作在处理某些问题时非常有用，比如某某个问题中，我们需要找出所有子区间的异或和等于2^x的数量。使用前缀异或和可以快速地计算出任意子区间的异或和，从而解决问题。

代码

#include <iostream> 
#include <vector>   using namespace std;// 函数：计算前缀异或和
vector<int> prefixXor(const vector<int>& nums) {vector<int> prefixXor(nums.size() + 1, 0); // 初始化前缀异或和数组，长度为nums.size() + 1，初始值为0for (int i = 1; i <= nums.size(); ++i) { // 从1开始遍历到nums.size()，计算前缀异或和prefixXor[i] = prefixXor[i - 1] ^ nums[i - 1]; // 当前位置的前缀异或和等于前一个位置的前缀异或和与当前元素的异或}return prefixXor; // 返回计算好的前缀异或和数组
}// 函数：计算异或和为2^x的子区间数量
int countSubarraysWithXor(vector<int>& prefixXor, int n, int x) {int count = 0; // 初始化计数器，用于统计符合条件的子区间数量int length = 1 << x; // 计算子区间的长度，即2^xfor (int start = 0; start <= n - length; ++start) { // 遍历所有可能的子区间起始位置int xorValue = prefixXor[start + length] ^ prefixXor[start]; // 计算子区间的异或和if (xorValue == (1 << x)) { // 如果子区间的异或和等于2^xcount++; // 增加计数器}}return count; // 返回符合条件的子区间数量
}int main() {int n; // 定义数组长度变量cin >> n; // 从标准输入读取数组长度vector<int> nums(n); // 创建一个向量来存储数组元素for (int i = 0; i < n; ++i) { // 遍历数组，从标准输入读取每个元素cin >> nums[i];}vector<int> prefixXor = prefixXor(nums); // 调用函数计算前缀异或和for (int x = 0; x <= 18; ++x) { // 遍历所有可能的x值，即2^xcout << countSubarraysWithXor(prefixXor, n, x) << endl; // 调用函数计算并输出每个x对应的子区间数量}return 0;
}