点一下关注吧！！！非常感谢！！持续更新！！！

目前已经更新到了：

• Hadoop（已更完）
• HDFS（已更完）
• MapReduce（已更完）
• Hive（已更完）
• Flume（已更完）
• Sqoop（已更完）
• Zookeeper（已更完）
• HBase（已更完）
• Redis （已更完）
• Kafka（已更完）
• Spark（已更完）
• Flink（已更完）
• ClickHouse（已更完）
• Kudu（已更完）
• Druid（已更完）
• Kylin（已更完）
• Elasticsearch（已更完）
• DataX（已更完）
• Tez（已更完）
• 数据挖掘（正在更新…）

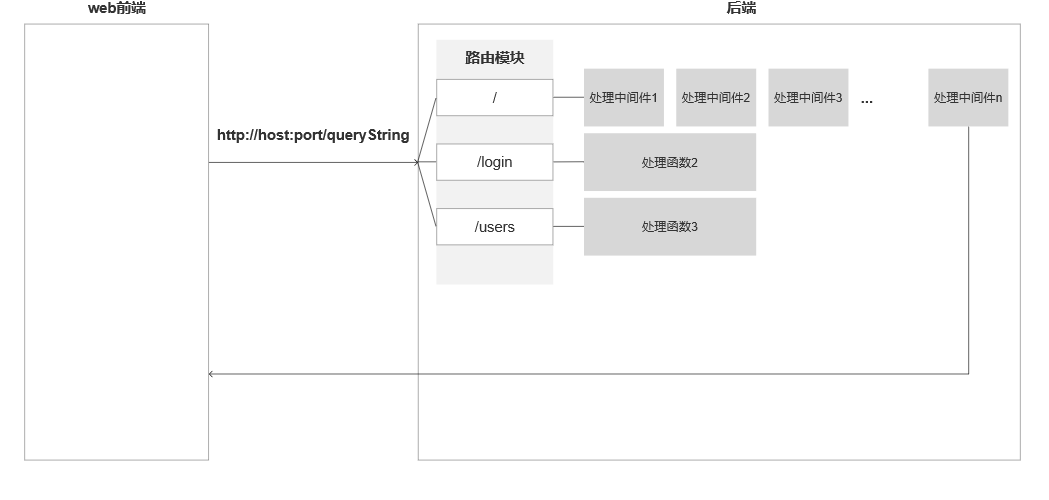
章节内容

上节我们完成了如下的内容：

• 线性回归
• 最小二乘法
• 多元线性

多元线性回归实现

利用矩阵乘法编写回归算法

多元线性回归的执行函数编写并不复杂，主要设计大量的矩阵计算，需要借助 Numpy 中的矩阵数据格式来完成。
首先执行标准导入：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

执行结果如下图所示，如果报错可能是缺少了库，需要安装：

编写线性回归函数，同理，我们假设输入数据集为 DataFrame，且最后一列为标签值：

def standRegres(dataSet):xMat = np.mat(dataSet.iloc[:,:-1].values) # 提取特征yMat = np.mat(dataSet.iloc[:,-1].values).T # 提取标签xTx = xMat.T*xMatif np.linalg.det(xTx) ==0:print('This matrix is singular,cannot do inverse') #行列式为0,则该矩阵为奇异矩阵,无法求解逆矩阵returnws = xTx.I * (xMat.T*yMat)return ws

这里需要判断 XTX 是否为满秩矩阵，若不满秩，则无法对其进行求逆矩阵的操作。定义函数后，即可测试运行效果，此处我们建立线性随机数进行多元线性回归方程拟合。这里需要注意的是，当使用矩阵分解来求解多元线性回归方程时，必须添加一列全为 1 的列，用于表征线性方程截距W0。

rng = np.random.RandomState(1) # 设置随机种子
x = 5*rng.rand(100) # 100个[0,5)的随机数
y = 2*x-5+rng.randn(100) # 真实规律的标签取值
X = pd.DataFrame(x)
Y = pd.DataFrame(y)
ex = pd.DataFrame(np.ones([100,1])) #添加一列权威1的列,表示截距
data = pd.concat([ex,X,Y],axis=1)

数据满足基本的建模要求，然后执行函数运算：

ws = standRegres(data)
ws

执行结果如下图所示：

返回结果即为各列特征权重，其中数据集第一列值均为 1，因此返回结果的第一个分量表示截距，然后可以用可视化图形展示模型拟合效果：

yhat = data.iloc[:,:-1].values*ws # 预测标签值
plt.plot(data.iloc[:,1],data.iloc[:,2],'o') #原始数据点
plt.plot(data.iloc[:,1],yhat) # 拟合直线

执行结果如下图所示：

算法评估指标

残差平方和 SSE，其计算公式如下：
其中的 m 为数据集记录书，yi 为实际标签值，y^为预测值，则可利用下面表达式进行计算：

y = data.iloc[:,-1].values
yhat = yhat.flatten()
SSE = np.power(yhat-y,2).sum()
print(SSE)

执行结果如下图所示：

当然也可以编写成一个完整的函数，为提高服用性，设置输入参数为数据集和回归方法：

def sseCal(dataSet,regres):n = dataSet.shape[0]y = dataSet.iloc[:,-1].valuesws = regres(dataSet)yhat = dataSet.iloc[:,:-1].values*wsyhat = yhat.flatten()SSE = np.power(yhat-y,2).sum()return SSE

测试运行：

sseCal(data,standRegres)

执行结果如下：

同时，在回归算法中，为了消除数据集规模对残差平方和的影响，往往我们会计算平均残差 MSE：

其中 m 为数据集样例个数，以及 RMSE 误差的均方根，为 MSE 开平方后所得结果。当然除此之外最常用的还是 R - square 判定系数，判定系数的计算需要使用之前介绍的组间误差平方和与离差平方和的概念。
在回归分析中，SSR 表示聚类中类似的组间平方和概念，译为：Sum of squares of the regression，由预测数据与标签均值之间差值的平方和构成。

而 SST （Total sum of squares）则是实际值和均值之间的差值的平方和：

对比之前介绍的聚类分析，此处可对比理解为以点聚点。同样，和轮廓系数类似，最终的判断系数表也同时结合了“组内误差”和“组件误差”两个指标。

判定系数 R方 测度了回归直线对观测数据的拟合程度：

• 若所有观测点都落在了直线上，残差平方和为 SSE = 0，则 R 方 = 1，拟合是完全的
• 如果 y 的变化与 x 无关，完全无助于解释 y 的变差，R 方 = 0。

可见 R 方的取值范围是 [0,1]：

• R 方越接近 1，表明回归平方和占总平方和的比例越大，回归直线与各个观测点越接近，用 x 的变化来解释 y 值变差（取值的波动称为变差）的部分越多，回归直线的拟合程度就越好。
• 反之，R 方越接近 0，回归直线的拟合程度就越差。

接下来，尝试计算上述拟合结果的判定系数：

sse = sseCal(data,standRegres)
y = data.iloc[:,-1].values
sst = np.power(y-y.mean(),2).sum()
1-sse/sst

执行结果如下所示：

结果为 0.91，能够看出最终拟合效果非常好，当然，我们也可以编写函数封装计算判断系数的相关操作，同样留一个调整回归函数的接口。

def rSquare(dataSet,regres):
sse = sseCal(dataSet,regres)
y = dataSet.iloc[:,-1].values
sst = np.power(y-y.mean(),2).sum()
return 1-sse/sst

然后进行测试

rSquare(data,standRegres)

执行结果如下图所示：