Day15刷算法

110.平衡二叉树

力扣题目链接(opens new window)

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

110.平衡二叉树

返回 true 。

class Solution {/*** 递归法*/public boolean isBalanced(TreeNode root) {return getHeight(root) != -1;}private int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);if (leftHeight == -1) {return -1;}int rightHeight = getHeight(root.right);if (rightHeight == -1) {return -1;}// 左右子树高度差大于1，return -1表示已经不是平衡树了if (Math.abs(leftHeight - rightHeight) > 1) {return -1;}return Math.max(leftHeight, rightHeight) + 1;}
}

我遇到的问题

1.本题中根据后序的逻辑，是从叶子节点递归调用还是从根节点呢 ？

在递归遍历二叉树时，最先达到的是叶子节点（因为每次递归调用都会先处理子节点），但这些叶子节点的信息会逐级向上传递，直到根节点。

具体来说，在这个平衡二叉树的检查算法中：

  1. 递归调用顺序：首先，递归会深入到最左边的叶子节点，然后逐级向上返回，接着再深入到右子树的最左边叶子节点，如此往复，直到遍历完整棵树。这是后序遍历的特性，即先处理左子树，再处理右子树，最后处理根节点（但在这个场景中，我们实际上并没有在根节点做额外的处理，而是在返回的过程中进行了平衡性的检查）。

  2. 检查过程：虽然递归调用是从根节点开始的，但实际的检查（即比较左右子树的高度）是在递归调用的返回过程中进行的。当递归调用到达叶子节点时（即 root == null 的情况），它会返回高度 0。然后，这个信息会逐级向上传递，每一层都会基于其子节点的高度来计算自己的高度，并检查是否平衡。

  3. 信息传递：叶子节点的高度（0）会作为递归调用的返回值逐级向上传递。在传递过程中，每一层都会检查当前节点是否平衡，并据此返回 -1（不平衡）或当前子树的高度（平衡）。

  4. 结果确定：最终，当递归调用返回到根节点时，isBalanced 方法会根据 getHeight(root) 的返回值来确定整个树是否平衡。

所以，检查是在向叶子节点遍历的过程中进行的，但信息传递和结果确定是从叶子节点逐级向上到根节点的”。

现在我们讲个故事来理解这个过程

想象您正在一棵二叉树中行走，从根节点开始。您的任务是检查这棵树是否平衡（即任何节点的两个子树的高度差不超过1）。

  1. 向叶子节点遍历：
    • 您首先走向根节点的左子树。
    • 在左子树中，您继续向左走，直到到达一个叶子节点（没有子节点的节点）。
    • 到达叶子节点后，您知道这个节点的高度是0。
    • 然后，您返回上一级，并向右走，继续这个过程，直到您检查了左子树中的所有节点。
    • 接着，您回到根节点，并重复这个过程，但这次是检查右子树。

       在这个过程中，您实际上是在向叶子节点遍历，并在这个过程中进行平衡性的检查（尽管实际的检查是在返回过程中基于子树的高度进行的）。

  1. 信息传递和结果确定：
    • 当您到达一个叶子节点并确定其高度为0时，这个信息会“传递”给它的父节点。
    • 父节点会基于其左右子树的高度（这些高度是通过递归调用得到的）来计算自己的高度，并检查是否平衡。
    • 如果父节点平衡，它会将自己的高度信息“传递”给它的父节点，依此类推，直到根节点。
    • 最终，当所有递归调用都返回时，根节点会知道整棵树是否平衡。

这个过程就像是您在树中行走时，不断地收集信息（子树的高度），并在返回时基于这些信息做出决策（树是否平衡）。

对于叶子节点来说：

  • 当 root 为某个叶子节点时，它的 left 和 right 指针中至少有一个（通常是两个）是 null。
  • 当递归调用到达这个 null 指针时，会返回 0。
  • 这个 0 会作为递归调用的结果返回给上一层调用，即成为上一层调用中 leftHeight 或 rightHeight 的值。

257. 二叉树的所有路径

力扣题目链接(opens new window)

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例: 

257.二叉树的所有路径1

思路

这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

前序遍历以及回溯的过程如图：

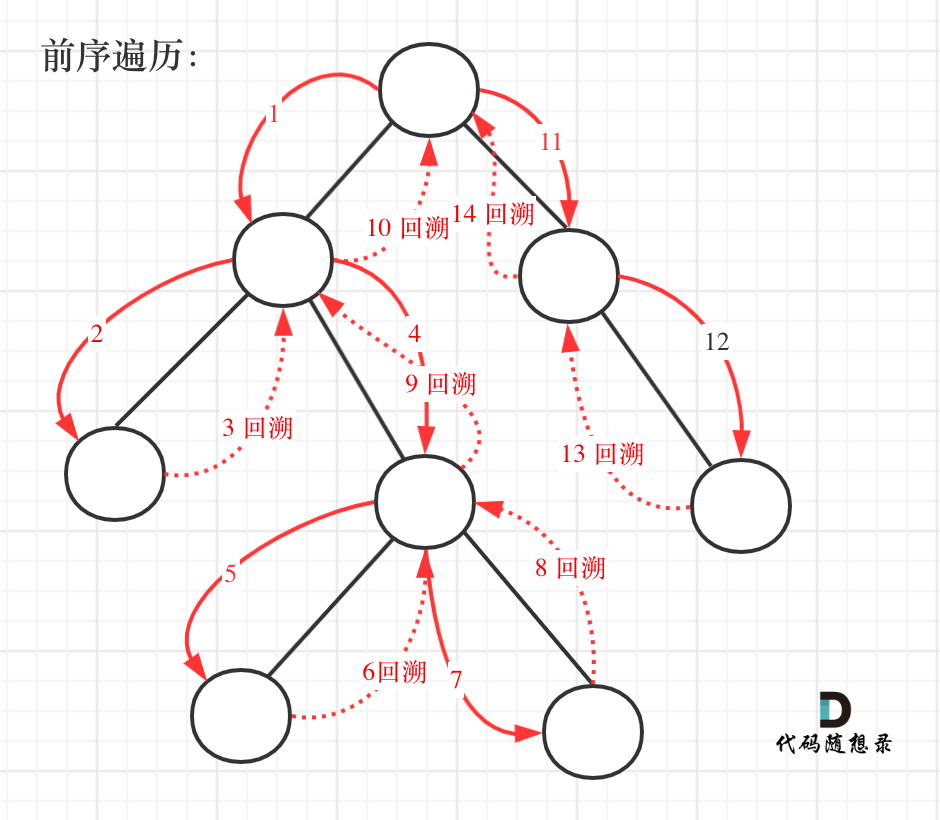
257.二叉树的所有路径

我们先使用递归的方式，来做前序遍历。要知道递归和回溯就是一家的，本题也需要回溯。

class Solution {/*** 递归法*/public List<String> binaryTreePaths(TreeNode root) {List<String> res = new ArrayList<>();// 存最终的结果if (root == null) {return res;}List<Integer> paths = new ArrayList<>();// 作为结果中的路径traversal(root, paths, res);return res;}private void traversal(TreeNode root, List<Integer> paths, List<String> res) {paths.add(root.val);// 前序遍历，中// 遇到叶子结点if (root.left == null && root.right == null) {// 输出StringBuilder sb = new StringBuilder();// StringBuilder用来拼接字符串，速度更快for (int i = 0; i < paths.size() - 1; i++) {sb.append(paths.get(i)).append("->");}sb.append(paths.get(paths.size() - 1));// 记录最后一个节点res.add(sb.toString());// 收集一个路径return;}// 递归和回溯是同时进行，所以要放在同一个花括号里if (root.left != null) { // 左traversal(root.left, paths, res);paths.remove(paths.size() - 1);// 回溯}if (root.right != null) { // 右traversal(root.right, paths, res);paths.remove(paths.size() - 1);// 回溯}}
}

404.左叶子之和

力扣题目链接(opens new window)

计算给定二叉树的所有左叶子之和。

示例：

404.左叶子之和1

思路

首先要注意是判断左叶子，不是二叉树左侧节点，所以不要上来想着层序遍历。

因为题目中其实没有说清楚左叶子究竟是什么节点，那么我来给出左叶子的明确定义：节点A的左孩子不为空，且左孩子的左右孩子都为空（说明是叶子节点），那么A节点的左孩子为左叶子节点

大家思考一下如下图中二叉树，左叶子之和究竟是多少？

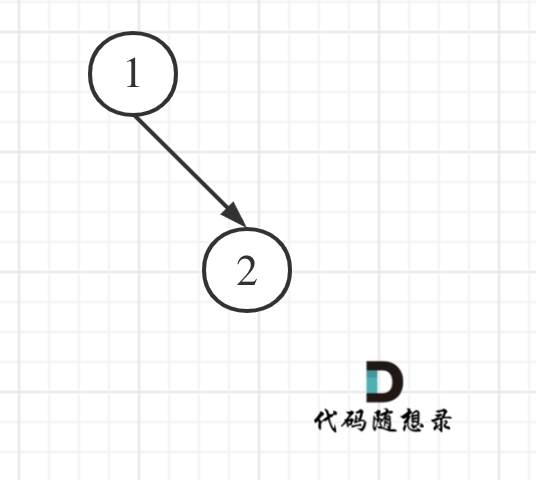
404.左叶子之和

 其实是0，因为这棵树根本没有左叶子！

但看这个图的左叶子之和是多少？

图二

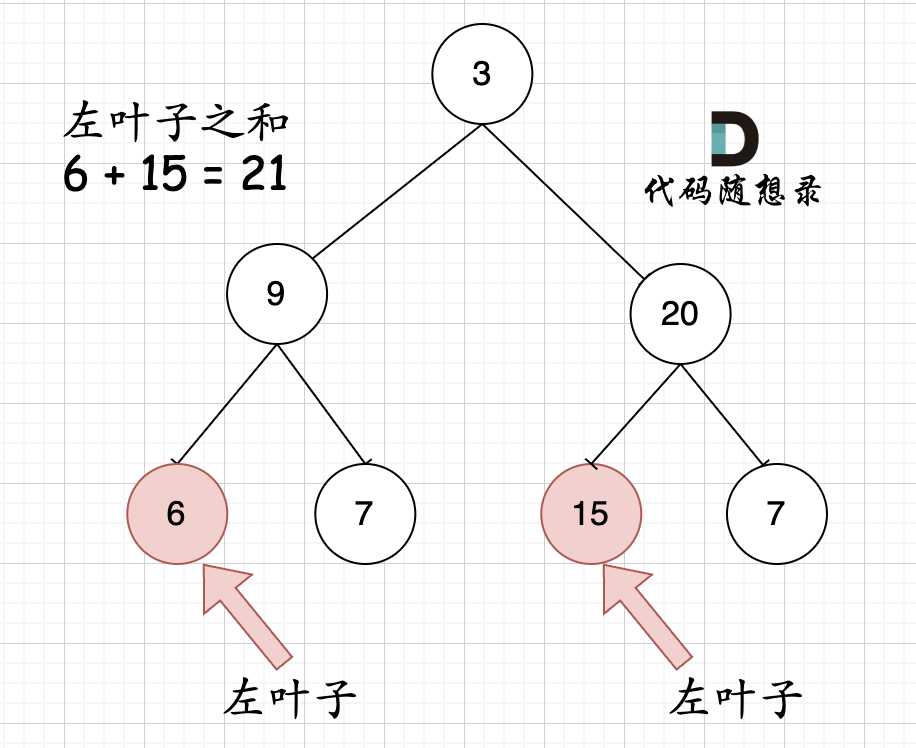
相信通过这两个图，大家对最左叶子的定义有明确理解了。

递归法

递归的遍历顺序为后序遍历（左右中），是因为要通过递归函数的返回值来累加求取左叶子数值之和。

递归三部曲：

  1. 确定递归函数的参数和返回值

判断一个树的左叶子节点之和，那么一定要传入树的根节点，递归函数的返回值为数值之和，所以为int

使用题目中给出的函数就可以了。

  1. 确定终止条件

如果遍历到空节点，那么左叶子值一定是0

if (root == NULL) return 0;

注意，只有当前遍历的节点是父节点，才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点，那其左叶子也必定是0，那么终止条件为：

if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0; //其实这个也可以不写，如果不写不影响结果，但就会让递归多进行了一层。
  1. 确定单层递归的逻辑

当遇到左叶子节点的时候，记录数值，然后通过递归求取左子树左叶子之和，和 右子树左叶子之和，相加便是整个树的左叶子之和。

class Solution {public int sumOfLeftLeaves(TreeNode root) {if (root == null) return 0;int leftValue = sumOfLeftLeaves(root.left);    // 左int rightValue = sumOfLeftLeaves(root.right);  // 右int midValue = 0;if (root.left != null && root.left.left == null && root.left.right == null) { midValue = root.left.val;}int sum = midValue + leftValue + rightValue;  // 中return sum;}
}

我遇到的问题 

1. sum = midValue + leftValue + rightValue; sum为什么要这么求

在sumOfLeftLeaves方法中，int sum = midValue + leftValue + rightValue;这行代码是用来计算并存储当前节点及其左右子树中所有左叶子节点的值之和的。

让我们逐一看看这些变量：

  1. midValue：
    • 这个变量用来存储当前节点的左子节点（如果它是一个左叶子节点）的值。
    • 如果当前节点的左子节点存在且没有自己的子节点（即它是一个叶子节点），则midValue会被设置为这个左叶子节点的值。
    • 如果当前节点的左子节点不存在或不是叶子节点，则midValue保持为0。
  2. leftValue：
    • 这个变量是通过递归调用sumOfLeftLeaves方法计算得到的，它表示当前节点的左子树中所有左叶子节点的值之和。
    • 如果当前节点没有左子节点，则leftValue为0（因为递归的基准情况会返回0）。
  3. rightValue：
    • 类似于leftValue，这个变量是通过递归调用sumOfLeftLeaves方法计算得到的，它表示当前节点的右子树中所有左叶子节点的值之和。
    • 注意这里有点微妙：即使我们是在考虑左叶子节点，我们仍然需要递归地检查右子树，因为右子树中可能包含作为其父节点左子节点的叶子节点（即这些叶子节点在它们自己的父节点看来是左叶子节点）。然而，由于我们只对“左叶子节点”感兴趣，并且这个定义是相对于它们的直接父节点而言的，所以右子树中的这些左叶子节点仍然会被正确地计算在内。

现在，int sum = midValue + leftValue + rightValue;这行代码将这三个值相加，得到当前节点及其左右子树中所有左叶子节点的值之和。这个总和随后被返回给上一层递归调用，直到最终到达根节点，此时得到的总和就是整个二叉树中所有左叶子节点的值之和。

简而言之，这行代码是递归过程中计算总和的关键步骤，它结合了当前节点的左叶子节点值（如果有的话）、左子树中所有左叶子节点的值之和以及右子树中所有左叶子节点的值之和。

222.完全二叉树的节点个数

力扣题目链接(opens new window)

给出一个完全二叉树，求出该树的节点个数。

示例 1：

  • 输入：root = [1,2,3,4,5,6]
  • 输出：6

示例 2：

  • 输入：root = []
  • 输出：0

示例 3：

  • 输入：root = [1]
  • 输出：1

提示：

  • 树中节点的数目范围是[0, 5 * 10^4]
  • 0 <= Node.val <= 5 * 10^4
  • 题目数据保证输入的树是 完全二叉树

普通二叉树

首先按照普通二叉树的逻辑来求。

这道题目的递归法和求二叉树的深度写法类似， 递归遍历的顺序依然是后序（左右中）。

#递归
  1. 确定递归函数的参数和返回值：参数就是传入树的根节点，返回就返回以该节点为根节点二叉树的节点数量，所以返回值为int类型。

先用c分步骤写出

代码如下：

int getNodesNum(TreeNode* cur) {
  1. 确定终止条件：如果为空节点的话，就返回0，表示节点数为0。

代码如下：

if (cur == NULL) return 0;
  1. 确定单层递归的逻辑：先求它的左子树的节点数量，再求右子树的节点数量，最后取总和再加一 （加1是因为算上当前中间节点）就是目前节点为根节点的节点数量。

代码如下：

int leftNum = getNodesNum(cur->left);      // 左
int rightNum = getNodesNum(cur->right);    // 右
int treeNum = leftNum + rightNum + 1;      // 中
return treeNum;

完全二叉树

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。

来举一个典型的例子如题：

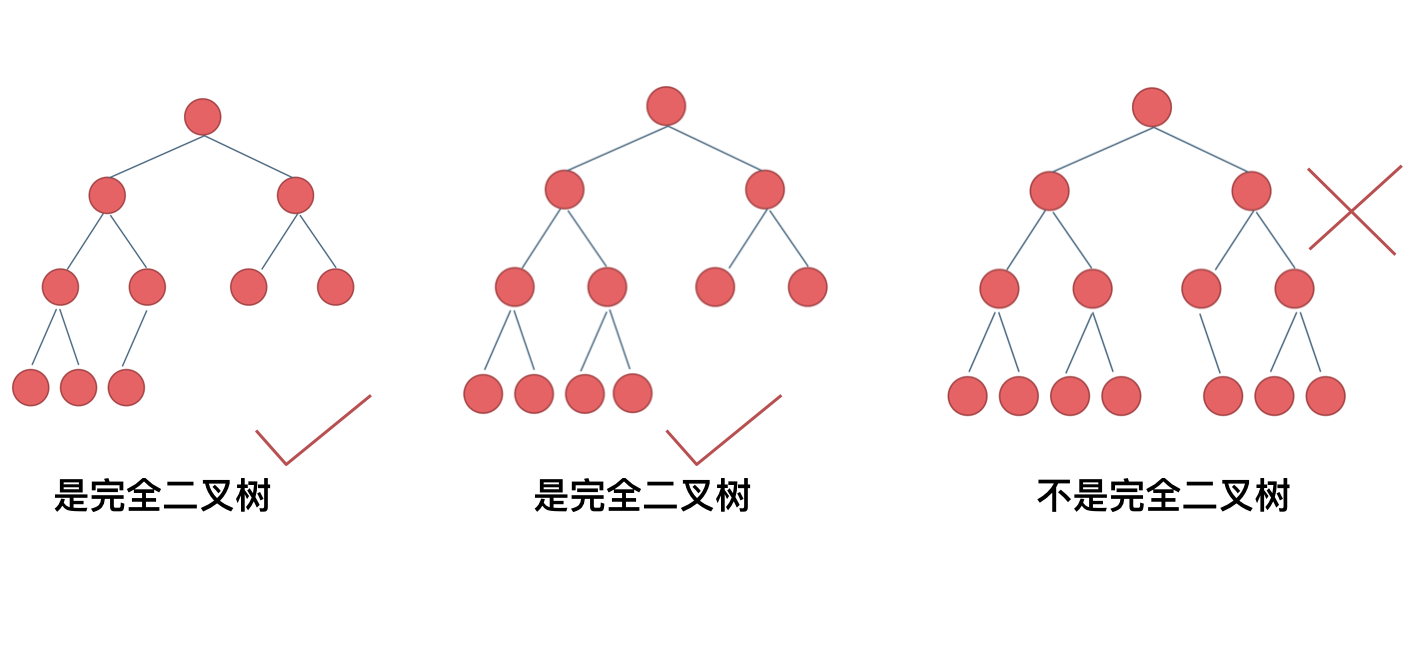
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

完全二叉树（一）如图： 

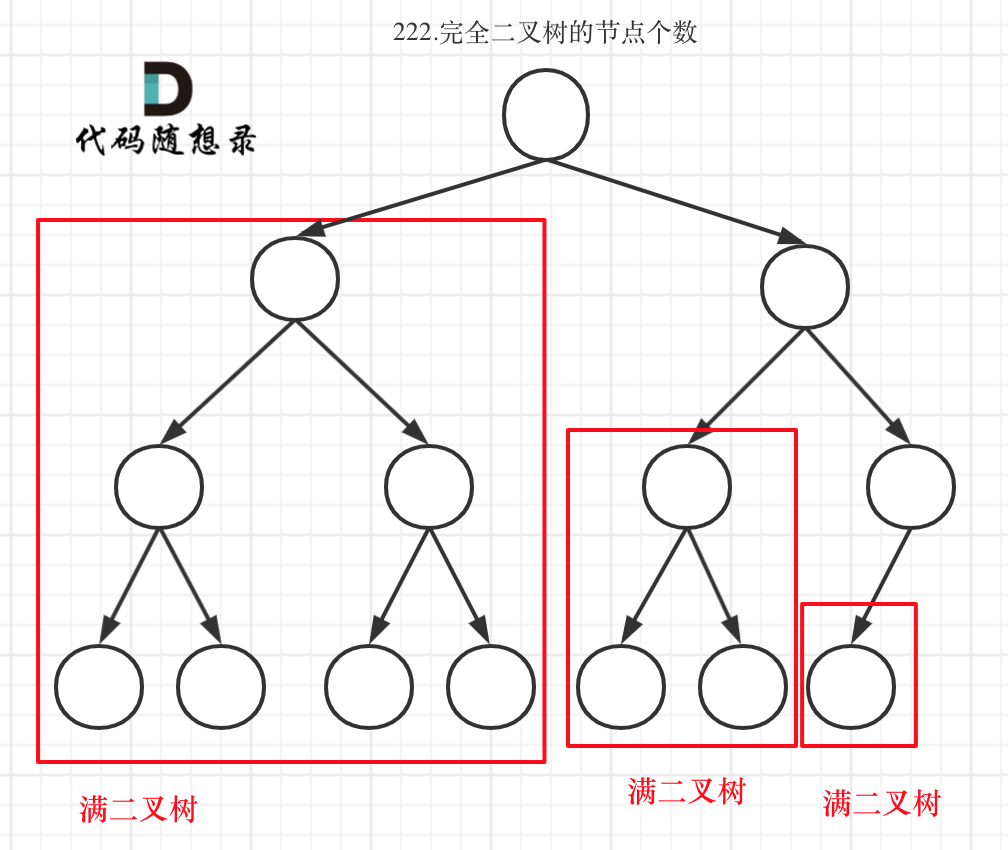
222.完全二叉树的节点个数

完全二叉树（二）如图： 

222.完全二叉树的节点个数1

可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：

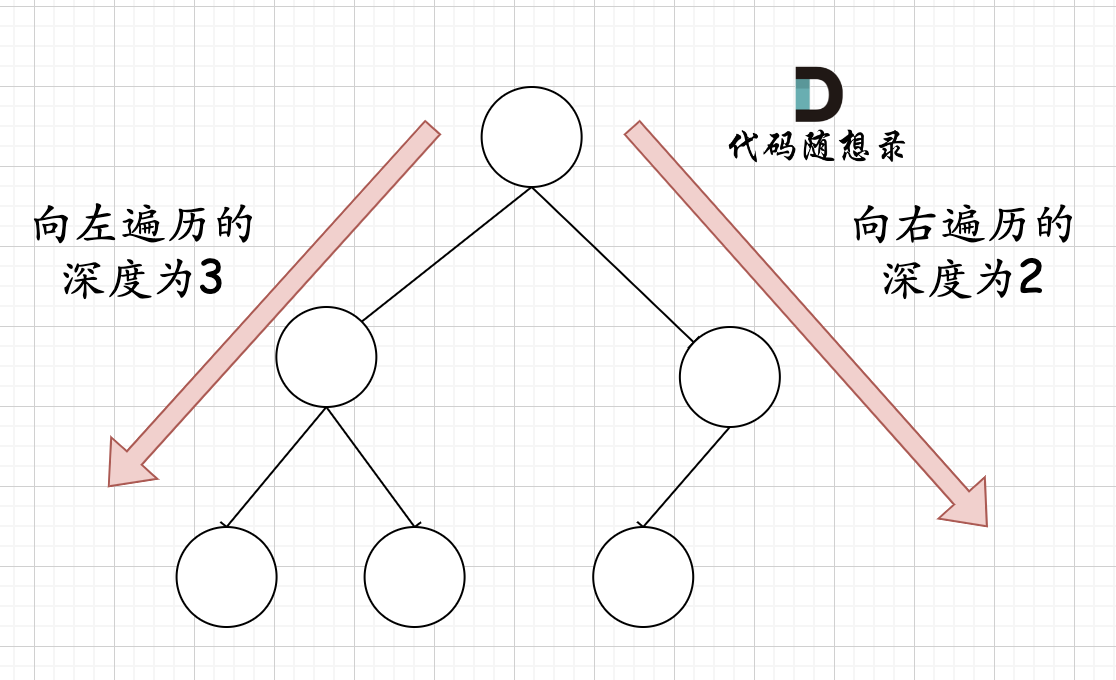
class Solution {/*** 针对完全二叉树的解法** 满二叉树的结点数为：2^depth - 1*/public int countNodes(TreeNode root) {if (root == null) return 0;TreeNode left = root.left;TreeNode right = root.right;int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便while (left != null) {  // 求左子树深度left = left.left;leftDepth++;}while (right != null) { // 求右子树深度right = right.right;rightDepth++;}if (leftDepth == rightDepth) {return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0}return countNodes(root.left) + countNodes(root.right) + 1;}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.xdnf.cn/news/20680.html

如若内容造成侵权/违法违规/事实不符，请联系一条长河网进行投诉反馈，一经查实，立即删除！

相关文章

命令执行简单

命令执行简单

前言&#xff1a;小迪安全2022第一节反弹shell&#xff0c;小迪用的是两台都是云服务器&#xff0c;没有服务器可以在自己的主机上搭建也是可以的&#xff0c;主机上搭两个网站 思路&#xff1a;生成一个木马文件&#xff0c;下载到本机&#xff0c;然后利用本机上传到目标主机…
阅读更多...
爆发的AI智能体（1）：学习AI智能体的计划和提纲

爆发的AI智能体（1）：学习AI智能体的计划和提纲

学习计划&#xff1a; 基础知识阶段&#xff08;1-2个月&#xff09;&#xff1a; 建立AI大模型的基础知识体系&#xff0c;包括理解AI智能体的基本概念及其与大模型&#xff08;如GPT、通义千问&#xff09;结合后的功能。学习AI智能体的关键构成&#xff0c;如大模型、规划&a…
阅读更多...
Vue 专属状态管理库Pinia的使用与实践

Vue 专属状态管理库Pinia的使用与实践

目录 前言1. 什么是 Pinia&#xff1f;2. Pinia 的安装与基本配置2.1 安装 Pinia2.2 在 Vue 应用中配置 Pinia 3. 使用 Pinia 创建和管理状态3.1 定义一个简单的 Store3.2 在组件中使用 Store 4. Pinia 的高级功能4.1 使用 Getter 简化数据处理4.2 支持异步操作4.3 在服务端渲染…
阅读更多...
springBoot插件打包部署

springBoot插件打包部署

打包插件spring-boot-maven-plugin 不使用插件&#xff0c;运行时&#xff0c;异常信息为“没有主清单属性” 本地部署 杀进程
阅读更多...
python使用poetry作为包管理

python使用poetry作为包管理

一、pip的弊端 由于Python使用pip安装时不会自动解决冲突&#xff0c;不会自动删除相关联的包&#xff0c;例如安装flask时&#xff0c;pip install flask会额外安装一些包&#xff0c;但是pip uninstall是不会删除相关的包&#xff0c;只会删除flask本身的包。 二、推荐使用…
阅读更多...
神经网络中常用的激活函数（公式 + 函数图像）

神经网络中常用的激活函数（公式 + 函数图像）

激活函数是人工神经网络中的一个关键组件&#xff0c;负责引入非线性&#xff0c;从而使神经网络能够学习和表示复杂的非线性关系。没有激活函数&#xff0c;神经网络中的所有计算都是线性变换&#xff0c;而线性模型的表达能力有限&#xff0c;无法处理复杂的任务。 激活函数…
阅读更多...
mysql复习题（实验7-8）

mysql复习题（实验7-8）

建立一个学生入学信息管理&#xff08;x_y&#xff09;数据库&#xff0c;设计其数据库模式为&#xff1a; 学生表&#xff08;学号&#xff0c;姓名&#xff0c;性别&#xff0c;入学成绩&#xff0c;籍贯&#xff0c;院系编号&#xff09; 院系表&#xff08;院系编号&…
阅读更多...
n个整数后移m个位置

n个整数后移m个位置

题目描述 有n个整数&#xff0c;使前面各数顺序向后移m个位置&#xff0c;最后m个数变成前面m个数&#xff0c;见图。写一函数&#xff1a;实现以上功能&#xff0c;在主函数中输入n个数和输出调整后的n个数。 输入描述 输入数据的个数n n个整数 移动的位置m 输出描述 移动后的…
阅读更多...
Python——面向过程和面向对象

Python——面向过程和面向对象

一.两大编程思想 面向过程&#xff1a;事情比较简单&#xff0c;可以用线性的思维去解决问题。例&#xff1a;c语言。 面向对象&#xff1a;事情比较复杂&#xff0c;使用简单的线性思维无法解决。例&#xff1a;python。 二.面向对象 1.类和对象 类和对象&#xff1a;由无…
阅读更多...
【机器学习】---神经架构搜索（NAS）

【机器学习】---神经架构搜索（NAS）

这里写目录标题 引言1. 什么是神经架构搜索&#xff08;NAS&#xff09;1.1 为什么需要NAS&#xff1f; 2. NAS的三大组件2.1 搜索空间搜索空间设计的考虑因素&#xff1a; 2.2 搜索策略2.3 性能估计 3. NAS的主要方法3.1 基于强化学习的NAS3.2 基于进化算法的NAS3.3 基于梯度的…
阅读更多...
图像上显示中文文本 - python 实现

图像上显示中文文本 - python 实现

该示例是在图像上显示中文文本&#xff0c;并用opencv的显示方式显示。 注意&#xff1a;SimHei.ttf&#xff08;黑体字体&#xff09;为字体文件&#xff0c;Windows 默认字体路径&#xff1a;C:/Windows/Fonts/SimHei.ttf 具体实现代码如下&#xff1a; # -*-coding:utf-8…
阅读更多...
dotnet:依赖注入

dotnet:依赖注入

依赖注入的基本概念 依赖&#xff1a;一个类依赖于另一个类或接口来完成其功能。注入&#xff1a;依赖项由外部提供给类&#xff0c;而不是由类自己创建。 builder.Services.AddScoped<IMyDependency, MyDependency>(); 这行代码使用 AddScoped 方法将 IMyDependency 接…
阅读更多...
JAVA题目笔记（十七）TreeSet对象排序+Map集合练习

JAVA题目笔记（十七）TreeSet对象排序+Map集合练习

一、TreeSet对象排序&#xff1a; 需求&#xff1a; public class Student implements Comparable<Student>{private String name;private int age;private int grade_Yu;private int grade_Shu;private int grade_Yin;private int sumthis.grade_Yinthis.grade_Shuthis…
阅读更多...
w046基于web的古典舞在线交流平台的设计与实现

w046基于web的古典舞在线交流平台的设计与实现

&#x1f64a;作者简介&#xff1a;多年一线开发工作经验&#xff0c;原创团队&#xff0c;分享技术代码帮助学生学习&#xff0c;独立完成自己的网站项目。 代码可以查看文章末尾⬇️联系方式获取&#xff0c;记得注明来意哦~&#x1f339;赠送计算机毕业设计600个选题excel文…
阅读更多...
【迅为】瑞芯微-RK3568开发板Linux+HAL启动测试

【迅为】瑞芯微-RK3568开发板Linux+HAL启动测试

迅为iTOP&#xff0d;RK3568开发板AMP AMP SDK支持Rockchip平台异构多系统AMP&#xff08;非对称多核架构&#xff09;的开发软件包&#xff0c;支持Linux(Kernel)、Standalone(Hal)、RTOS(RT-Thread)组合AMP构建形式。可以满足一些特定行业应用&#xff0c;如电力物联网、电…
阅读更多...
渗透测试--Windows系统下的文件传输手段

渗透测试--Windows系统下的文件传输手段

很多情况下&#xff0c;我们渗透测试都面临需要上传和下载文件的文件传输需求。本文专门探讨Windows服务器或主机上实施文件传输的各种方案。该专题比较敏感&#xff0c;该文章仅供学习使用&#xff0c;不要用于非法用途。 编码方法 Linux检查文件MD5 md5sum id_rsa Linux编…
阅读更多...
视觉常用Backbone大全：VisionTransformer（ViT）

视觉常用Backbone大全：VisionTransformer（ViT）

视觉常用Backbone大全 今天介绍的主干网络模型叫VisionTransformer&#xff0c;是一种将 Transformer 架构应用于计算机视觉任务的模型&#xff0c;通过将图像进行切块&#xff0c;将图片转变为self-attention认识的token输入到Transformer模块中&#xff0c;实现了Transformer…
阅读更多...
星海智算：Stable Diffusion3.5镜像教程

星海智算：Stable Diffusion3.5镜像教程

Stable Diffusion3.5 模型介绍 Stable Diffusion 3.5是由Stability AI推出的最新图像生成模型&#xff0c;它是Stable Diffusion系列中的一个重大升级。这个模型家族包括三个版本&#xff0c;分别是Stable Diffusion 3.5 Large、Stable Diffusion 3.5 Large Turbo和Stable Dif…
阅读更多...
[JavaWeb] 尚硅谷JavaWeb课程笔记

[JavaWeb] 尚硅谷JavaWeb课程笔记

1 Tomcat服务器 Tomcat目录结构 bin&#xff1a;该目录下存放的是二进制可执行文件&#xff0c;如果是安装版&#xff0c;那么这个目录下会有两个exe文件&#xff1a;tomcat10.exe、tomcat10w.exe&#xff0c;前者是在控制台下启动Tomcat&#xff0c;后者是弹出GUI窗口启动To…
阅读更多...
【Unity基础】认识Unity中的包

【Unity基础】认识Unity中的包

Unity中的包是一个核心概念&#xff0c;像Unity本身的功能的扩展&#xff0c;或者项目中资源的管理&#xff0c;都是通过包的形式来实现的。 一、什么是包&#xff1f; 一个包包含满足您项目各种需求的功能。这可以包括编辑器安装过程中附带的任何核心Unity功能&#xff0c;也…
阅读更多...
最新文章

Copyright @ 2022~2023