强化学习之基于模型的算法之动态规划
动态规划(Dynamic Programming, DP)是解决马尔可夫决策过程(MDP)的核心方法之一,通过自举(Bootstrapping)和递归更新实现最优策略的求解。
网格环境
以下是自定义的网格环境代码
from typing import Union
import matplotlib.animation as animation
import matplotlib.patches as patches
import matplotlib.pyplot as plt
import numpy as npnp.random.seed(1)
class Render:def __init__(self, target: Union[list, tuple, np.ndarray], forbidden: Union[list, tuple, np.ndarray],size=5):""" Render 类的构造函数:param target:目标点的位置:param forbidden:障碍物区域位置:param size:网格世界的size 默认为 5x5"""# 初始化self.agent = Noneself.target = targetself.forbidden = forbiddenself.size = sizeself.fig = plt.figure(figsize=(10, 10), dpi=self.size * 20)self.ax = plt.gca()self.ax.xaxis.set_ticks_position('top')self.ax.invert_yaxis()self.ax.xaxis.set_ticks(range(0, size + 1))self.ax.yaxis.set_ticks(range(0, size + 1))self.ax.grid(True, linestyle="-", color="gray", linewidth="1", axis='both')self.ax.tick_params(bottom=False, left=False, right=False, top=False, labelbottom=False, labelleft=False,labeltop=False)# 绘制网格世界的state index 以及grid边框的标号# index = 0for y in range(size):self.write_word(pos=(-0.6, y), word=str(y + 1), size_discount=0.8)self.write_word(pos=(y, -0.6), word=str(y + 1), size_discount=0.8)# for x in range(size):# self.write_word(pos=(x, y), word="s" + str(index), size_discount=0.65)# index += 1# 填充障碍物和目标格子for pos in self.forbidden:self.fill_block(pos=pos)self.fill_block(pos=self.target, color='darkturquoise')self.trajectory = []self.agent = patches.Arrow(-10, -10, 0.4, 0, color='red', width=0.5)self.ax.add_patch(self.agent)def fill_block(self, pos: Union[list, tuple, np.ndarray], color: str = '#EDB120', width=1.0,height=1.0) -> patches.RegularPolygon:"""对指定pos的网格填充颜色:param width::param height::param pos: 需要填充的网格的左下坐标:param color: 填充的颜色 默认为‘EDB120’表示 forbidden 格子 ,‘#4DBEEE’表示 target 格子:return: Rectangle对象"""return self.ax.add_patch(patches.Rectangle((pos[0], pos[1]),width=1.0,height=1.0,facecolor=color,fill=True,alpha=0.90,))def draw_random_line(self, pos1: Union[list, tuple, np.ndarray], pos2: Union[list, tuple, np.ndarray]) -> None:"""在pos1 和pos2之间生成一条线条,这条线条会在pos1和pos2之间产生随机偏移:param pos1: 起点所在位置的坐标:param pos2: 终点所在位置的坐标:return:None"""offset1 = np.random.uniform(low=-0.05, high=0.05, size=1)offset2 = np.random.uniform(low=-0.05, high=0.05, size=1)x = [pos1[0] + 0.5, pos2[0] + 0.5]y = [pos1[1] + 0.5, pos2[1] + 0.5]if pos1[0] == pos2[0]:x = [x[0] + offset1, x[1] + offset2]else:y = [y[0] + offset1, y[1] + offset2]self.ax.plot(x, y, color='g', scalex=False, scaley=False)def draw_circle(self, pos: Union[list, tuple, np.ndarray], radius: float,color: str = 'green', fill: bool = True) -> patches.CirclePolygon:"""对指定pos的网格内画一个圆:param fill: 是否填充圆的内部:param radius: 圆的半径:param pos: 需要画圆的网格的左下坐标:param color: 'lime'表示 绿色:return: CirclePolygon"""return self.ax.add_patch(patches.Circle((pos[0] + 0.5, pos[1] + 0.5),radius=radius,facecolor=color,edgecolor='green',linewidth=2,fill=fill))def draw_action(self, pos: Union[list, tuple, np.ndarray], toward: Union[list, tuple, np.ndarray],color: str = 'green', radius: float = 0.10) -> None:"""将动作可视化:param radius: circle 的半径:param pos:网格的左下坐标:param toward:(a,b) a b 分别表示 箭头在x方向和y方向的分量 如果是一个 0 向量就画圆:param color: 箭头的颜色 默认为green:return:None"""if not np.array_equal(np.array(toward), np.array([0, 0])):self.ax.add_patch(patches.Arrow(pos[0] + 0.5, pos[1] + 0.5, dx=toward[0],dy=toward[1], color=color, width=0.05 + 0.05 * np.linalg.norm(np.array(toward) / 0.5),linewidth=0.5))else:self.draw_circle(pos=tuple(pos), color='white', radius=radius, fill=False)def write_word(self, pos: Union[list, np.ndarray, tuple], word: str, color: str = 'black', y_offset: float = 0,size_discount: float = 1.0) -> None:"""在网格上对应位置写字:param pos: 需要写字的格子的左下角坐标:param word: 要写的字:param color: 字的颜色:param y_offset: 字在y方向上关于网格中心的偏移:param size_discount: 字体大小 (0-1):return: None"""self.ax.text(pos[0] + 0.5, pos[1] + 0.5 + y_offset, word, size=size_discount * (30 - 2 * self.size), ha='center',va='center', color=color)def upgrade_agent(self, pos: Union[list, np.ndarray, tuple], action,next_pos: Union[list, np.ndarray, tuple], ) -> None:"""更新agent的位置:param next_pos: 当前pos和下一步的位置:param action: 对应位置采取的action:param pos: 当前的state位置:return: None"""self.trajectory.append([tuple(pos), action, tuple(next_pos)])def show_frame(self, t: float = 0.2) -> None:"""显示figure 持续一段时间后 关闭:param t: 持续时间:return: None"""self.fig.show()def save_frame(self, name: str) -> None:"""将当前帧保存:param name:保存的文件名:return: None"""self.fig.savefig(name + ".jpg")def save_video(self, name: str) -> None:"""如果指定了起点 想要将agent从起点到终点的轨迹show出来的话,可以使用这个函数保存视频:param name:视频文件的名字:return:None"""anim = animation.FuncAnimation(self.fig, self.animate, init_func=self.init(), frames=len(self.trajectory),interval=25, repeat=False)anim.save(name + '.mp4')# init 和 animate 都是服务于animation.FuncAnimation# 具体用法参考matplotlib官网def init(self):passdef animate(self, i):print(i,len(self.trajectory))location = self.trajectory[i][0]action = self.trajectory[i][1]next_location = self.trajectory[i][2]next_location = np.clip(next_location, -0.4, self.size - 0.6)self.agent.remove()if action[0] + action[1] != 0:self.agent = patches.Arrow(x=location[0] + 0.5, y=location[1] + 0.5,dx=action[0] / 2, dy=action[1] / 2,color='b',width=0.5)else:self.agent = patches.Circle(xy=(location[0] + 0.5, location[1] + 0.5),radius=0.15, fill=True, color='b',)self.ax.add_patch(self.agent)self.draw_random_line(pos1=location, pos2=next_location)def draw_episode(self):for i in range(len(self.trajectory)):location = self.trajectory[i][0]next_location = self.trajectory[i][2]self.draw_random_line(pos1=location, pos2=next_location)def add_subplot_to_fig(self, fig, x, y, subplot_position, xlabel, ylabel, title=''):"""在给定的位置上添加一个子图到当前的图中,并在子图中调用plot函数,设置x,y label和title。参数:x: 用于plot的x数据y: 用于plot的y数据subplot_position: 子图的位置,格式为 (row, column, index)xlabel: x轴的标签ylabel: y轴的标签title: 子图的标题"""# 在指定位置添加子图ax = fig.add_subplot(subplot_position)# 调用plot函数绘制图形ax.plot(x, y)# 设置x,y label和titleax.set_xlabel(xlabel)ax.set_ylabel(ylabel)ax.set_title(title)def draw_loss(self,losses):# 绘制损失图plt.plot(range(len(losses)), losses)plt.xlabel('Iteration')plt.ylabel('Loss')plt.title('Policy Iteration Loss')plt.show()if __name__ == '__main__':render = Render(target=[4, 4], forbidden=[np.array([1, 2]), np.array([2, 2])], size=5)render.draw_action(pos=[3, 3], toward=(0, 0.4))# render.save_frame('test1')for num in range(10):render.draw_random_line(pos1=[1.5, 1.5], pos2=[1.5, 2.5])action_to_direction = {0: np.array([-1, 0]),1: np.array([0, 1]),2: np.array([1, 0]),3: np.array([0, -1]),4: np.array([0, 0]),}# uniform_policy = np.random.random(size=(25, 5))uniform_policy = np.ones(shape=(25, 5)) / 5for state in range(25):for action in range(5):policy = uniform_policy[state, action]render.draw_action(pos=[state // 5, state % 5], toward=policy * 0.4 * action_to_direction[action],radius=0.03 + 0.07 * policy)for a in range(5):render.trajectory.append((a, a))render.show_frame()
import time
from typing import Optional, Union, List, Tupleimport gym
import numpy as np
from gym import spaces
from gym.core import RenderFrame, ActType, ObsType
np.random.seed(1)
import render#检查array是否存在_list中
def arr_in_list(array, _list):for element in _list:if np.array_equal(element, array):return Truereturn Falseclass GridEnv(gym.Env):def __init__(self, size: int, target: Union[list, tuple, np.ndarray], forbidden: Union[list, tuple, np.ndarray],render_mode: str):"""GridEnv 的构造函数:param size: grid_world 的边长:param target: 目标点的pos:param forbidden: 不可通行区域 二维数组 或者嵌套列表 如 [[1,2],[2,2]]:param render_mode: 渲染模式 video表示保存视频"""# 初始化可视化self.agent_location = np.array([0, 0])self.time_steps = 0self.size = sizeself.render_mode = render_modeself.render_ = render.Render(target=target, forbidden=forbidden, size=size)# 初始化起点 障碍物 目标点self.forbidden_location = []for fob in forbidden:self.forbidden_location.append(np.array(fob))self.target_location = np.array(target)# 初始化 动作空间 观测空间self.action_space, self.action_space_size = spaces.Discrete(5), spaces.Discrete(5).nself.reward_list = [0, 1, -10, -10]self.observation_space = spaces.Dict({"agent": spaces.Box(0, size - 1, shape=(2,), dtype=int),"target": spaces.Box(0, size - 1, shape=(2,), dtype=int),"barrier": spaces.Box(0, size - 1, shape=(2,), dtype=int),})# action to pos偏移量 的一个mapself.action_to_direction = {0: np.array([-1, 0]), #上1: np.array([0, 1]), #右2: np.array([1, 0]), #下3: np.array([0, -1]), #左4: np.array([0, 0]), #原地}# Rsa表示 在 指定 state 选取指点 action 得到reward的概率self.Rsa = None# Psa表示 在 指定 state 选取指点 action 跳到下一个state的概率self.Psa = Noneself.psa_rsa_init()def reset(self, *, seed: Optional[int] = None, options: Optional[dict] = None, ) -> Tuple[ObsType, dict]:super().reset(seed=seed)self.agent_location = np.array([0, 0])observation = self.get_obs()info = self.get_info()return observation, infodef step(self, action: ActType) -> Tuple[ObsType, float, bool, bool, dict]:reward = self.reward_list[self.Rsa[self.pos2state(self.agent_location), action].tolist().index(1)]direction = self.action_to_direction[action]self.render_.upgrade_agent(self.agent_location, direction, self.agent_location + direction)self.agent_location = np.clip(self.agent_location + direction, 0, self.size - 1)terminated = np.array_equal(self.agent_location, self.target_location)observation = self.get_obs()info = self.get_info()return observation, reward, terminated, False, infodef render(self) -> Optional[Union[RenderFrame, List[RenderFrame]]]:if self.render_mode == "video":self.render_.save_video('image/' + str(time.time()))self.render_.show_frame(0.3)return Nonedef get_obs(self) -> ObsType:return {"agent": self.agent_location, "target": self.target_location, "barrier": self.forbidden_location}def get_info(self) -> dict:return {"time_steps": self.time_steps}#将位置索引转换为二维坐标def state2pos(self, state: int) -> np.ndarray:return np.array((state // self.size, state % self.size))#将二维坐标转换为位置索引def pos2state(self, pos: np.ndarray) -> int:return pos[0] * self.size + pos[1]def psa_rsa_init(self):"""初始化网格世界的 psa 和 rsa:return:"""state_size = self.size ** 2self.Psa = np.zeros(shape=(state_size, self.action_space_size, state_size), dtype=float)self.Rsa = np.zeros(shape=(self.size ** 2, self.action_space_size, len(self.reward_list)), dtype=float)for state_index in range(state_size):for action_index in range(self.action_space_size):pos = self.state2pos(state_index)next_pos = pos + self.action_to_direction[action_index]if next_pos[0] < 0 or next_pos[1] < 0 or next_pos[0] > self.size - 1 or next_pos[1] > self.size - 1:self.Psa[state_index, action_index, state_index] = 1 #表示超出边界后仍保留在当前状态self.Rsa[state_index, action_index, 3] = 1else:self.Psa[state_index, action_index, self.pos2state(next_pos)] = 1if np.array_equal(next_pos, self.target_location):self.Rsa[state_index, action_index, 1] = 1elif arr_in_list(next_pos, self.forbidden_location):self.Rsa[state_index, action_index, 2] = 1else:self.Rsa[state_index, action_index, 0] = 1def close(self):passif __name__ == "__main__":grid = GridEnv(size=5, target=[1, 2], forbidden=[[2, 2],[3,3]]], render_mode='')grid.render()

1)值迭代(Value Iteration, VI)
核心思想
- 直接优化状态价值函数:通过反复迭代贝尔曼最优方程,逐步逼近最优价值函数 V∗。
- 贪心策略改进:在每一步更新后,直接根据当前价值函数生成最优策略(无需显式策略评估)。
伪代码
初始化
- 已知所有状态-动作对的概率模型 p(r∣s,a) 和 p(s′∣s,a)。
- 初始猜测 v0 作为初始状态值函数。
目标
- 搜索最优状态值函数 v∗ 和一个最优策略 π∗,以解决贝尔曼最优性方程。
算法步骤
- 检查收敛性:
- 当 vk 尚未收敛(即 ∥vk−vk−1∥ 大于预定义的小阈值)时,进行第 k 次迭代。
- 遍历所有状态:
- 对于每一个状态 s∈S,执行以下步骤:
- 遍历所有动作:
- 对于每一个动作 a∈A(s),执行以下步骤:
- 计算 Q 值:
- 计算qk(s,a):
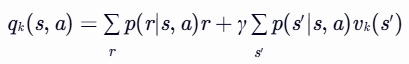
- 选择最大动作值:
- 找到使qk(s,a) 最大的动作 ak∗(s):

- 策略更新:
- 更新策略 πk+1(a∣s):

- 值函数更新:
- 更新状态值函数 vk+1(s):
实现代码
import time
import numpy as np
import grid_envclass Solve:def __init__(self, env: grid_env.GridEnv):self.gama = 0.9 #折扣因子,表示未来奖励的衰减程度self.env = envself.action_space_size = env.action_space_size #动作空间大小self.state_space_size = env.size ** 2 #状态空间大小self.reward_space_size, self.reward_list = len(self.env.reward_list), self.env.reward_list #奖励self.state_value = np.zeros(shape=self.state_space_size) #状态值self.qvalue = np.zeros(shape=(self.state_space_size, self.action_space_size)) #动作值self.mean_policy = np.ones(shape=(self.state_space_size, self.action_space_size)) / self.action_space_size #平均策略,表示采取每个动作概率相等self.policy = self.mean_policy.copy()def calculate_qvalue(self, state, action, state_value):"""计算q值:param state: 对应的state:param action: 对应的action:param state_value: 状态值:return: 计算出的结果"""qvalue = 0for i in range(self.reward_space_size):qvalue += self.reward_list[i] * self.env.Rsa[state, action, i]for next_state in range(self.state_space_size):qvalue += self.gama * self.env.Psa[state, action, next_state] * state_value[next_state]return qvaluedef policy_improvement(self, state_value):"""更新 qvalue ;qvalue[state,action]=reward+value[next_state]找到 state 处的 action*:action* = arg max(qvalue[state,action]) 即最优action即最大qvalue对应的action更新 policy :将 action*的概率设为1 其他action的概率设为0 这是一个greedy policy:param: state_value: policy对应的state value:return: improved policy, 以及迭代下一步的state_value"""policy = np.zeros(shape=(self.state_space_size, self.action_space_size))state_value_k = state_value.copy()for state in range(self.state_space_size): #2、遍历所有状态qvalue_list = []for action in range(self.action_space_size): #3、遍历所有动作qvalue_list.append(self.calculate_qvalue(state, action, state_value.copy())) #4、计算q值state_value_k[state] = max(qvalue_list)action_star = qvalue_list.index(max(qvalue_list)) #5、选择最大动作值policy[state, action_star] = 1 #6、策略更新return policy, state_value_kdef value_iteration(self, tolerance=0.001):"""迭代求解最优贝尔曼公式 得到 最优state value tolerance 和 steps 满足其一即可:param tolerance: 当 前后 state_value 的范数小于tolerance 则认为state_value 已经收敛:param steps: 当迭代次数大于step时 停止 建议将此变量设置大一些:return: 剩余迭代次数"""state_value_k = np.ones(self.state_space_size)while np.linalg.norm(state_value_k - self.state_value, ord=1) > tolerance: #1、检查收敛性self.state_value = state_value_k.copy()self.policy, state_value_k = self.policy_improvement(state_value_k.copy()) #7、值函数更新def show_policy(self):# 可视化策略(Policy):将智能体的策略(每次行动的方向标注为箭头)以图形化的方式渲染到环境中for state in range(self.state_space_size):for action in range(self.action_space_size):policy = self.policy[state, action]self.env.render_.draw_action(pos=self.env.state2pos(state),toward=policy * 0.4 * self.env.action_to_direction[action],radius=policy * 0.1)def show_state_value(self, state_value, y_offset=0.2):# 可视化状态价值函数(State - ValueFunction):将每个状态的价值(长期累积奖励的预期)以文本形式渲染到环境中。for state in range(self.state_space_size):self.env.render_.write_word(pos=self.env.state2pos(state), word=str(round(state_value[state], 1)),y_offset=y_offset,size_discount=0.7)if __name__ == "__main__":env = grid_env.GridEnv(size=5, target=[2, 3],forbidden=[[2, 2], [2, 1], [1, 1], [3, 3], [1, 3], [1, 4]],render_mode='')solver = Solve(env)start_time = time.time()solver.value_iteration()end_time = time.time()cost_time = end_time - start_timeprint("cost_time:{}".format(round(cost_time, 2)))solver.show_policy()solver.show_state_value(solver.state_value, y_offset=0.25)solver.env.render()效果

2)策略迭代(Policy Iteration, PI)
核心思想
- 交替优化策略与价值函数:
- 策略评估(Policy Evaluation):固定当前策略 π,计算其状态价值函数 Vπ。
- 策略改进(Policy Improvement):根据 Vπ 生成更优策略 π′。
伪代码
初始化
- 已知所有状态-动作对的概率模型 p(r∣s,a) 和 p(s′∣s,a)。
- 初始猜测策略 π0。
目标
- 搜索最优状态值函数 v∗ 和一个最优策略 π∗。
算法步骤
- 检查策略收敛性:
- 当策略 πk 尚未收敛时,进行第 k 次迭代。
- 策略评估:
- 初始化:任意初始猜测 v(0)。
- 在策略 πk 下,进行第 j 次迭代,直到 v(j) 收敛。
- 计算状态值函数:
- 对于每一个状态 s∈S,计算 vπk(j+1)(s):

- 策略改进:
- 对于每一个状态 s∈S,执行以下步骤:
- 对于每一个动作 a∈A(s),计算 qπk(s,a):

- 找到使qk(s,a) 最大的动作 ak∗(s):

- 更新策略 πk+1(a∣s):

实现代码
import time
import numpy as npimport grid_envclass Solve:def __init__(self, env: grid_env.GridEnv):self.gama = 0.9 #折扣因子,表示未来奖励的衰减程度self.env = envself.action_space_size = env.action_space_size #动作空间大小self.state_space_size = env.size ** 2 #状态空间大小self.reward_space_size, self.reward_list = len(self.env.reward_list), self.env.reward_list #奖励self.state_value = np.zeros(shape=self.state_space_size) #状态值self.qvalue = np.zeros(shape=(self.state_space_size, self.action_space_size)) #动作值self.mean_policy = np.ones(shape=(self.state_space_size, self.action_space_size)) / self.action_space_size #平均策略,表示采取每个动作概率相等self.policy = self.mean_policy.copy()def calculate_qvalue(self, state, action, state_value):"""计算q值:param state: 对应的state:param action: 对应的action:param state_value: 状态值:return: 计算出的结果"""qvalue = 0for i in range(self.reward_space_size):qvalue += self.reward_list[i] * self.env.Rsa[state, action, i]for next_state in range(self.state_space_size):qvalue += self.gama * self.env.Psa[state, action, next_state] * state_value[next_state]return qvaluedef policy_evaluation(self, policy, tolerance=0.001):"""策略评估迭代求解贝尔曼公式 得到 state value tolerance 和 steps 满足其一即可:param policy: 需要求解的policy:param tolerance: 当 前后 state_value 的范数小于tolerance 则认为state_value 已经收敛,收敛阈值:param steps: 当迭代次数大于step时 停止计算 此时若是policy iteration 则算法变为 truncated iteration:return: 求解之后的收敛值"""state_value_k = np.ones(self.state_space_size)state_value = np.zeros(self.state_space_size)# 用于计算两个向量(在这里是 state_value_k 和 state_value)之间的 L1 范数(曼哈顿距离)while np.linalg.norm(state_value_k - state_value, ord=1) > tolerance:state_value = state_value_k.copy()for state in range(self.state_space_size):value = 0for action in range(self.action_space_size):value += policy[state, action] * self.calculate_qvalue(state_value=state_value_k.copy(),state=state,action=action) # bootstrapping,是一种通过利用当前估计值来更新新估计值的技术,旨在减少对环境反馈的长期依赖,提高学习效率state_value_k[state] = valuereturn state_value_kdef policy_improvement(self, state_value):"""策略改进更新 qvalue ;qvalue[state,action]=reward+value[next_state]找到 state 处的 action*:action* = arg max(qvalue[state,action]) 即最优action即最大qvalue对应的action更新 policy :将 action*的概率设为1 其他action的概率设为0 这是一个greedy policy:param: state_value: policy对应的state value:return: improved policy, 以及迭代下一步的state_value"""policy = np.zeros(shape=(self.state_space_size, self.action_space_size))state_value_k = state_value.copy()for state in range(self.state_space_size):qvalue_list = []for action in range(self.action_space_size):qvalue_list.append(self.calculate_qvalue(state, action, state_value.copy())) #3、计算状态值state_value_k[state] = max(qvalue_list)action_star = qvalue_list.index(max(qvalue_list))policy[state, action_star] = 1return policy, state_value_kdef policy_iteration(self, tolerance=0.001):""":param tolerance: 迭代前后policy的范数小于tolerance 则认为已经收敛:param steps: step 小的时候就退化成了 truncated iteration:return: 剩余迭代次数"""policy = self.random_policy() #采用随机策略while np.linalg.norm(policy - self.policy, ord=1)>tolerance: #1、检查策略收敛性policy = self.policy.copy()self.state_value = self.policy_evaluation(self.policy.copy(), tolerance) #2、策略评估self.policy, _ = self.policy_improvement(self.state_value) #4、策略改进def random_policy(self):"""生成随机的策略,随机生成一个策略:return:"""policy = np.zeros(shape=(self.state_space_size, self.action_space_size))for state_index in range(self.state_space_size):action = np.random.choice(range(self.action_space_size))policy[state_index, action] = 1return policydef show_policy(self):for state in range(self.state_space_size):for action in range(self.action_space_size):policy = self.policy[state, action]self.env.render_.draw_action(pos=self.env.state2pos(state),toward=policy * 0.4 * self.env.action_to_direction[action],radius=policy * 0.1)def show_state_value(self, state_value, y_offset=0.2):for state in range(self.state_space_size):self.env.render_.write_word(pos=self.env.state2pos(state), word=str(round(state_value[state], 1)),y_offset=y_offset,size_discount=0.7)if __name__ == "__main__":env = grid_env.GridEnv(size=5, target=[2, 3],forbidden=[[2, 2], [2, 1], [1, 1], [3, 3], [1, 3], [1, 4]],render_mode='')solver = Solve(env)start_time = time.time()solver.policy_iteration()end_time = time.time()cost_time = end_time - start_timeprint("cost_time:{}".format(round(cost_time, 2)))solver.show_policy()solver.show_state_value(solver.state_value, y_offset=0.25)solver.env.render()效果

3)截断策略迭代(Truncated Policy Iteration, TPI)
核心思想
- 有限次策略评估:在策略迭代中,仅执行有限次(如 k 次)策略评估迭代,而非完全收敛。
- 平衡效率与精度:适用于大规模MDP,避免策略评估的过高计算成本。
伪代码
初始化
- 已知所有状态-动作对的概率模型 p(r∣s,a) 和 p(s′∣s,a)。
- 初始猜测策略 π0。
目标
- 搜索最优状态值函数 v∗ 和一个最优策略 π∗。
算法步骤
- 检查策略收敛性:
- 当策略 πk 尚未收敛时,进行第 k 次迭代。
- 策略评估:
- 初始化:选择初始猜测 vk(0)=vk−1。
- 设置最大迭代次数为 jtruncate。
- 进行策略评估:
- 当 j<jtruncate,执行以下步骤:
- 对于每一个状态 s∈S,计算 vk(j+1)(s):

- 设置 vk=vk(jtruncate)。
- 策略改进:
- 对于每一个状态 s∈S,执行以下步骤:
- 对于每一个动作 a∈A(s),计算 qπk(s,a):

- 找到使qk(s,a) 最大的动作 ak∗(s):

- 更新策略 πk+1(a∣s):

实现代码
import time
import numpy as npimport grid_envclass Solve:def __init__(self, env: grid_env.GridEnv):self.gama = 0.9 #折扣因子,表示未来奖励的衰减程度self.env = envself.action_space_size = env.action_space_size #动作空间大小self.state_space_size = env.size ** 2 #状态空间大小self.reward_space_size, self.reward_list = len(self.env.reward_list), self.env.reward_list #奖励self.state_value = np.zeros(shape=self.state_space_size) #状态值self.qvalue = np.zeros(shape=(self.state_space_size, self.action_space_size)) #动作值self.mean_policy = np.ones(shape=(self.state_space_size, self.action_space_size)) / self.action_space_size #平均策略,表示采取每个动作概率相等self.policy = self.mean_policy.copy()def calculate_qvalue(self, state, action, state_value):"""计算q值:param state: 对应的state:param action: 对应的action:param state_value: 状态值:return: 计算出的结果"""qvalue = 0for i in range(self.reward_space_size):qvalue += self.reward_list[i] * self.env.Rsa[state, action, i]for next_state in range(self.state_space_size):qvalue += self.gama * self.env.Psa[state, action, next_state] * state_value[next_state]return qvaluedef policy_evaluation(self, policy, tolerance=0.001, steps=100):"""策略评估迭代求解贝尔曼公式 得到 state value tolerance 和 steps 满足其一即可:param policy: 需要求解的policy:param tolerance: 当 前后 state_value 的范数小于tolerance 则认为state_value 已经收敛,收敛阈值:param steps: 当迭代次数大于step时 停止计算 此时若是policy iteration 则算法变为 truncated iteration:return: 求解之后的收敛值"""state_value_k = np.ones(self.state_space_size)state_value = np.zeros(self.state_space_size)while steps>0:steps -= 1state_value = state_value_k.copy()for state in range(self.state_space_size):value = 0for action in range(self.action_space_size):value += policy[state, action] * self.calculate_qvalue(state_value=state_value_k.copy(),state=state,action=action) # bootstrapping,是一种通过利用当前估计值来更新新估计值的技术,旨在减少对环境反馈的长期依赖,提高学习效率state_value_k[state] = valuereturn state_value_kdef policy_improvement(self, state_value):"""策略改进更新 qvalue ;qvalue[state,action]=reward+value[next_state]找到 state 处的 action*:action* = arg max(qvalue[state,action]) 即最优action即最大qvalue对应的action更新 policy :将 action*的概率设为1 其他action的概率设为0 这是一个greedy policy:param: state_value: policy对应的state value:return: improved policy, 以及迭代下一步的state_value"""policy = np.zeros(shape=(self.state_space_size, self.action_space_size))state_value_k = state_value.copy()for state in range(self.state_space_size):qvalue_list = []for action in range(self.action_space_size):qvalue_list.append(self.calculate_qvalue(state, action, state_value.copy()))state_value_k[state] = max(qvalue_list)action_star = qvalue_list.index(max(qvalue_list))policy[state, action_star] = 1return policy, state_value_kdef truncated_policy_iteration(self, tolerance=0.001):""":param tolerance: 迭代前后policy的范数小于tolerance 则认为已经收敛:param steps: step 小的时候就退化成了 truncated iteration:return: 剩余迭代次数"""policy = self.random_policy()while np.linalg.norm(policy - self.policy, ord=1)>tolerance: #1、检查策略收敛性policy = self.policy.copy()self.state_value = self.policy_evaluation(self.policy.copy(), tolerance, 100) #2、策略评估self.policy, _ = self.policy_improvement(self.state_value) #4、策略改进def random_policy(self):"""生成随机的策略,随机生成一个策略:return:"""policy = np.zeros(shape=(self.state_space_size, self.action_space_size))for state_index in range(self.state_space_size):action = np.random.choice(range(self.action_space_size))policy[state_index, action] = 1return policydef show_policy(self):for state in range(self.state_space_size):for action in range(self.action_space_size):policy = self.policy[state, action]self.env.render_.draw_action(pos=self.env.state2pos(state),toward=policy * 0.4 * self.env.action_to_direction[action],radius=policy * 0.1)def show_state_value(self, state_value, y_offset=0.2):for state in range(self.state_space_size):self.env.render_.write_word(pos=self.env.state2pos(state), word=str(round(state_value[state], 1)),y_offset=y_offset,size_discount=0.7)if __name__ == "__main__":env = grid_env.GridEnv(size=5, target=[2, 3],forbidden=[[2, 2], [2, 1], [1, 1], [3, 3], [1, 3], [1, 4]],render_mode='')solver = Solve(env)start_time = time.time()solver.truncated_policy_iteration()end_time = time.time()cost_time = end_time - start_timeprint("cost_time:{}".format(round(cost_time, 2)))solver.show_policy()solver.show_state_value(solver.state_value, y_offset=0.25)solver.env.render()效果

三者比较

