摘要
本文探讨了多种智能优化算法在路径规划中的应用,包括粒子群算法(PSO)、遗传算法(GA)、差分进化算法(DE)、灰狼优化算法(GWO)和麻雀优化算法(SSA)。通过对比不同算法的收敛速度、路径效率以及适应性,评估各算法在复杂路径规划问题中的表现。实验结果显示,各算法均能实现路径优化,但其收敛效果和优化效率存在显著差异。
理论
2. 粒子群算法(PSO)
PSO是一种基于群体协作的优化算法,通过模拟群体中个体之间的交互找到最优解。PSO在路径规划中可以快速收敛,但在复杂地形中易陷入局部最优。
2. 遗传算法(GA)
遗传算法通过遗传和选择机制对路径进行优化,通过交叉和变异产生新解。GA在路径规划中具有全局搜索能力,但收敛速度较慢。
3. 差分进化算法(DE)
DE算法通过差分向量的叠加来更新路径,具有较强的全局优化能力。在路径规划中,DE具有较好的收敛性和鲁棒性。
4. 灰狼优化算法(GWO)
GWO模仿狼群围猎行为,通过领导狼和跟随狼的合作来找到最优路径。GWO在复杂路径中表现较好,但在大规模问题中效率稍逊。
5. 麻雀优化算法(SSA)
SSA通过模拟麻雀觅食行为实现路径优化,具有较好的全局搜索能力。SSA在路径规划中表现稳定,能有效避免局部最优。
实验结果
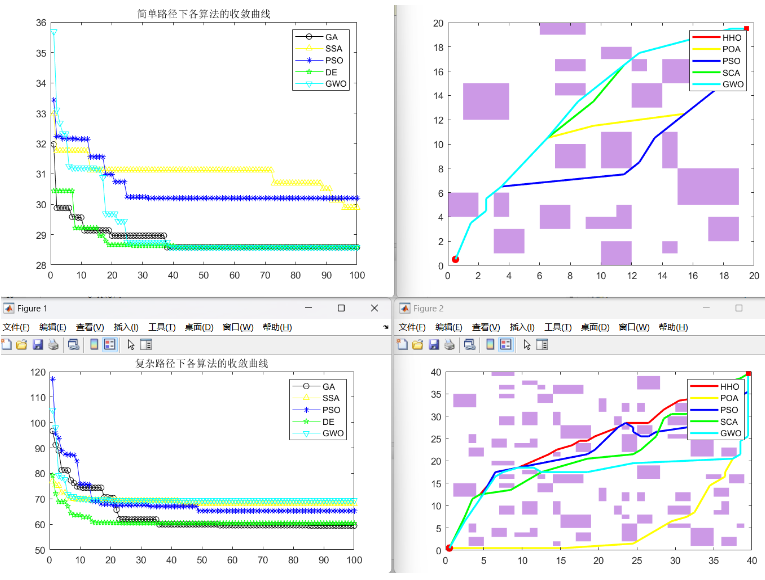
实验对比了五种算法在不同路径规划问题中的表现,实验结果图如上图所示。实验设置了两个场景:
1. 简单路径:障碍较少的路径规划环境
-
收敛速度:DE > GWO > PSO > SSA > GA
-
能耗优化:DE和GWO在简单路径中表现出较优的能耗节约效果。
2. 复杂路径:随机生成的复杂障碍物路径规划环境
-
收敛速度:HHO > POA > PSO > SCA > GWO
-
能耗优化:HHO和POA在复杂路径中表现出更强的适应性,能有效规避障碍。
部分代码
% 参数初始化
num_particles = 30; % 粒子数量
num_iterations = 100; % 迭代次数% 初始化粒子群位置和速度
position = rand(num_particles, 2) * max_range; % 初始位置
velocity = zeros(num_particles, 2); % 初始速度% 主循环
for iter = 1:num_iterationsfor i = 1:num_particles% 计算适应度fitness(i) = calculate_fitness(position(i, :));% 更新粒子速度和位置velocity(i, :) = update_velocity(position(i, :), global_best);position(i, :) = position(i, :) + velocity(i, :);end% 更新全局最优[global_best, fitness_best] = update_global_best(position, fitness);
end% 适应度计算函数
function fitness = calculate_fitness(position)% 根据路径长度和障碍物避让计算适应度% 实现代码...
end% 更新速度函数
function velocity = update_velocity(position, global_best)% 基于PSO公式更新速度% 实现代码...
end
参考文献
❝
Kennedy, J., & Eberhart, R. (1995). Particle swarm optimization. Proceedings of ICNN'95 - International Conference on Neural Networks, 4, 1942–1948.
Holland, J. H. (1992). Adaptation in Natural and Artificial Systems. MIT Press.
Storn, R., & Price, K. (1997). Differential Evolution – A simple and efficient heuristic for global optimization over continuous spaces. Journal of Global Optimization, 11(4), 341–359.
Mirjalili, S., & Lewis, A. (2014). Grey Wolf Optimizer. Advances in Engineering Software, 69, 46–61.
(文章内容仅供参考,具体效果以图片为准)