如下图所示,选择多条线并统计长度:
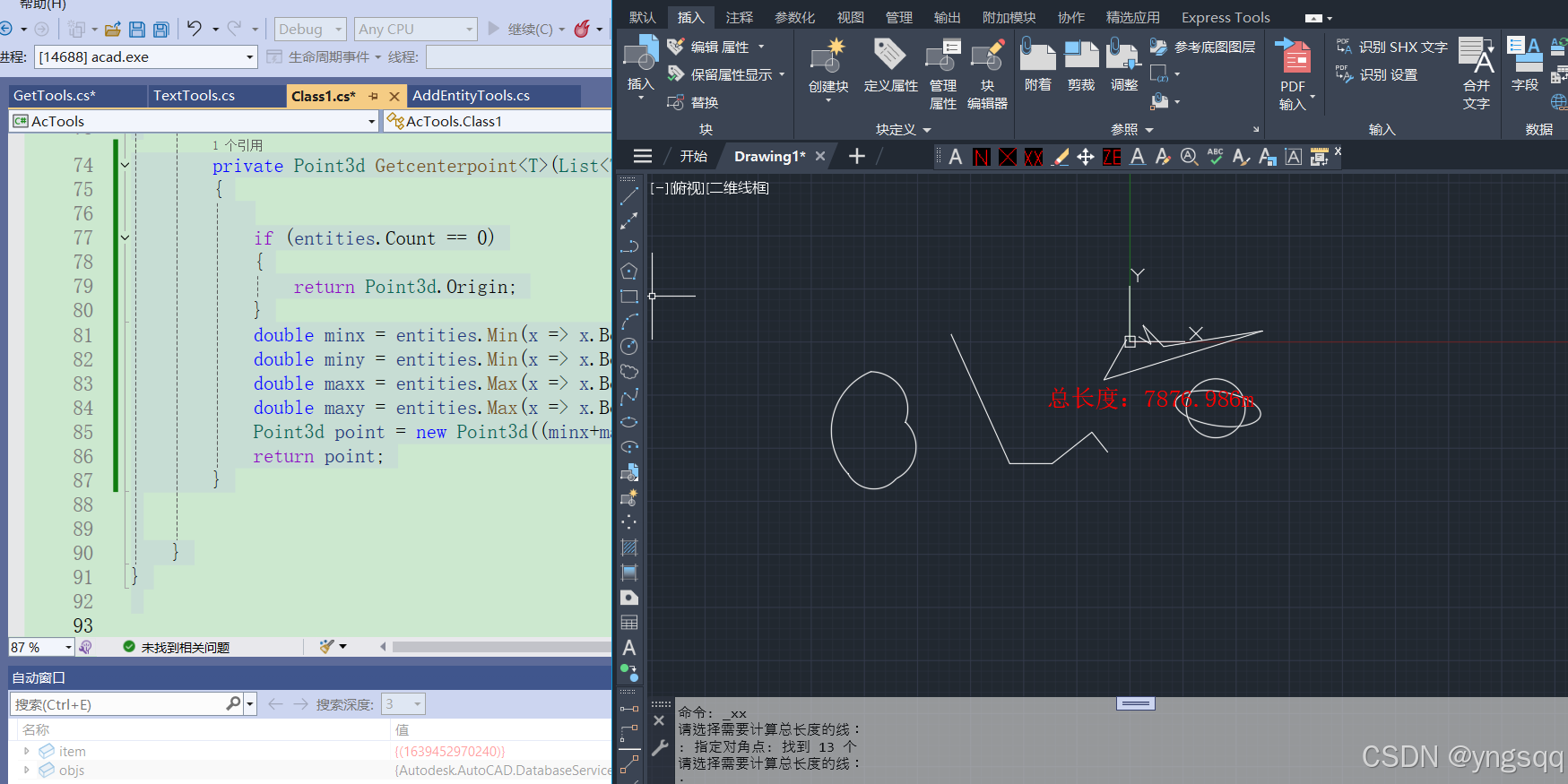
c#中不包含直接获取curve曲线长度 属性,需用如下方法:curve.GetDistanceAtParameter(item.EndParam)
附部分代码如下:
using Autodesk.AutoCAD.ApplicationServices;
using Autodesk.AutoCAD.DatabaseServices;
using Autodesk.AutoCAD.Geometry;
using Autodesk.AutoCAD.Runtime;
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using AcTools;
using Autodesk.AutoCAD.EditorInput;
using Autodesk.AutoCAD.Colors;
using System.Runtime.CompilerServices;
using Wform = System.Windows.Forms;
using System.IO;
using System.Windows.Forms;
//using Excel = NetOffice.ExcelApi;namespace AcTools
{public class Class1{#region //Polyline pl = new Polyline(3);//pl.AddVertexAt(0, new Point2d(10, 2), 0, 0, 0); // 起点 //pl.AddVertexAt(1, new Point2d(30, 5), 0, 0, 0); // 起点 //pl.AddVertexAt(2, new Point2d(50, 25), 0, 0, 0); // 起点 //Editor ed = Application.DocumentManager.MdiActiveDocument.Editor;//db.AddEntityToModeSpace(line);#endregion[CommandMethod("xx")]public void XX() {double sum = 0;Z.db.GetEntities1(out List<Curve> curves, "\n请选择需要计算总长度的线:\n");if (curves == null|curves.Count==0) return ;Point3d ps = Getcenterpoint(curves);foreach (var item in curves){sum = sum + item.GetDistanceAtParameter(item.EndParam);}//double sum3 = curves.Sum(x => x.GetDistanceAtParameter(x.EndParam));sum = Math.Round(sum, 3);//string sum2 = sum.ToString("f2");DBText text = new DBText() { Height = 100, Position =ps,TextString = $"总长度:{sum}m",ColorIndex= 1 };//DBText text2 = new DBText() { Position = ps, TextString = $"2:{sum2}㎡", ColorIndex = 2 };//DBText text3 = new DBText() { Position = ps, TextString = $"3:{sum3}㎡", ColorIndex = 3 };Z.db.AddEntityToModeSpace(text);//(text,text2,text3);Z.db.Zoom();}private List<double> Getboxs(List<Entity> entities){List< double> lis = new List< double>();if (entities.Count ==0){return lis;}double minx = entities.Min(x => x.Bounds.Value.MinPoint.X);double miny = entities.Min(x => x.Bounds.Value.MinPoint.Y);double maxx = entities.Max(x => x.Bounds.Value.MaxPoint.X);double maxy = entities.Max(x => x.Bounds.Value.MaxPoint.Y);lis.Add(minx);lis.Add(miny);lis.Add(maxx);lis.Add(maxy);return lis;}private Point3d Getcenterpoint<T>(List<T> entities) where T : Entity{if (entities.Count == 0){return Point3d.Origin;}double minx = entities.Min(x => x.Bounds.Value.MinPoint.X);double miny = entities.Min(x => x.Bounds.Value.MinPoint.Y);double maxx = entities.Max(x => x.Bounds.Value.MaxPoint.X);double maxy = entities.Max(x => x.Bounds.Value.MaxPoint.Y);Point3d point = new Point3d((minx+maxx)/2,(miny+maxy)/2,0);return point;}}
}代码包含部分本博自己封装函数,CAD二次开发、插件定制↓↓↓











![[MySQL#7] CRUD(2) | 更新 | 删除 | 聚合函数 | group by](https://img-blog.csdnimg.cn/img_convert/a3a2d3ae1b02550c3f839ec4145bb907.png)