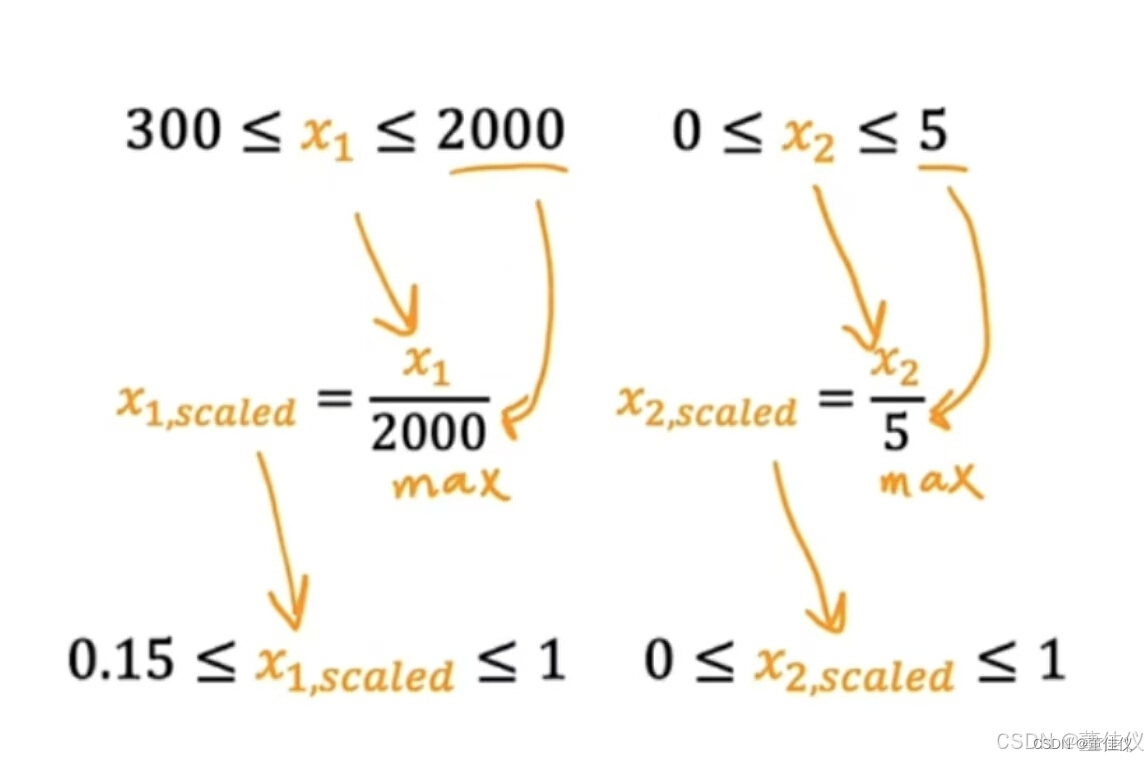
 两边同时除以最大范围,除了除以最大值以外,你还可以执行所谓的均值归一化。这看起来是,你从原始特征开始,然后你重新缩放他们,使两者其中以零为中心。以前它们只有大于零的值,现在他们既有负值又有正值这通常可能在负一和正一之间
两边同时除以最大范围,除了除以最大值以外,你还可以执行所谓的均值归一化。这看起来是,你从原始特征开始,然后你重新缩放他们,使两者其中以零为中心。以前它们只有大于零的值,现在他们既有负值又有正值这通常可能在负一和正一之间 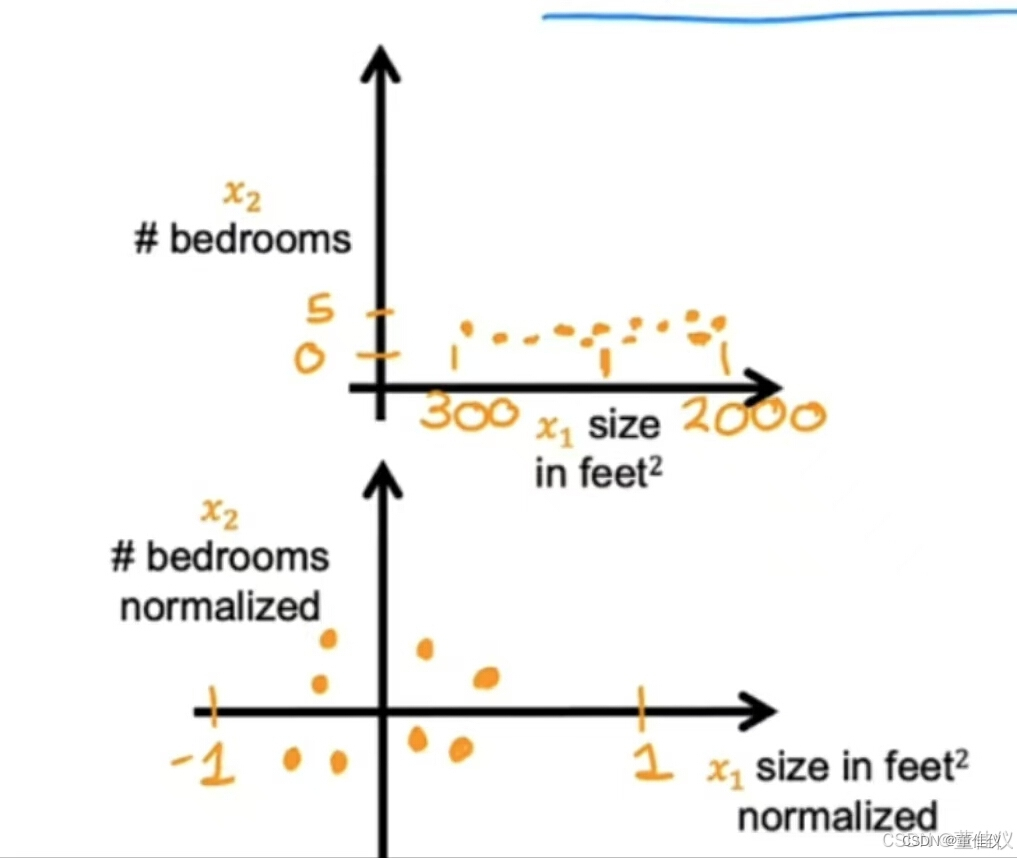
要计算x_1的均值归一化,首先求均值,也称为训练集上x_1的均值,我们称其为均值Mu_1,这是希腊字母Mu。假如你发现特征1的平均值,Mu_1是600平方英尺。让我们取每个x_1,减去平均Mu_1,然后让我们除以差值2000减去300,其中2000是最大值,300是最小值,如果你这样做,你会得到标准的x_1范围为负0.18—0.82。同样,要平均归一化x_2,你可以计算特征2的平均值。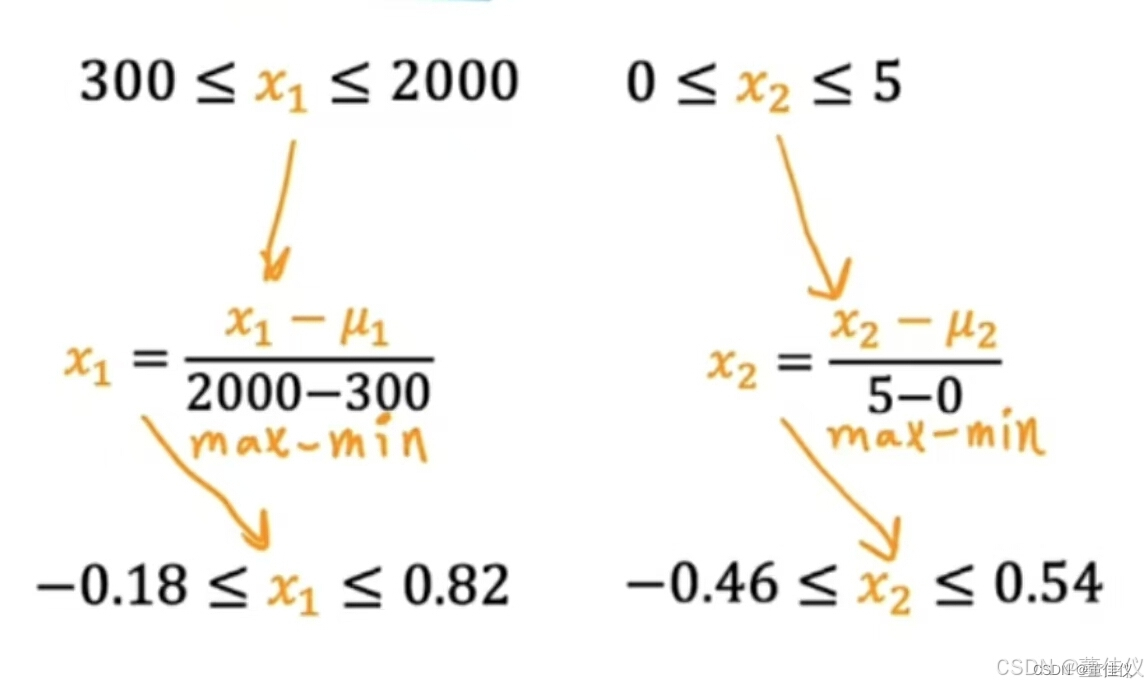
最后一个常见的重新缩放方法调用Z-score标准化。为了实现 Z-score归一化,需要计算每一个特征的标准差。如果不知道标准差是多少,不用担心一会会学习。或者你听说过正态分布或钟形曲线,有时也被称为高斯分布,这就是标准差对于正态分布的样子。如果你知道什么是标准差然后实现Z-score归一化,你首先计算平均Mu以及标准差,这通常由每个特征的小写希腊字母Sigma表示。。例,也许特征1的标准差为450,平均值为600,然后对Z-score归一化x_1,取每个x_1,减去Mu_1,然后除以标准差,我将其表示为Sigma1。你可能会发现Z分数已标准化x_1现在的范围为-0.67-3.1。同样如果计算第二个特征的标准差为1.4且均值为2.3,然后你可以计算x_2,减去Mu_2,然后除以Sigma2,在这种情况下,由x_2归一化的Z分数现在可能范围为-1.6-1.9。如果你将训练数据绘制在图上的归一化x_1和x_2上,他可能看起来像这样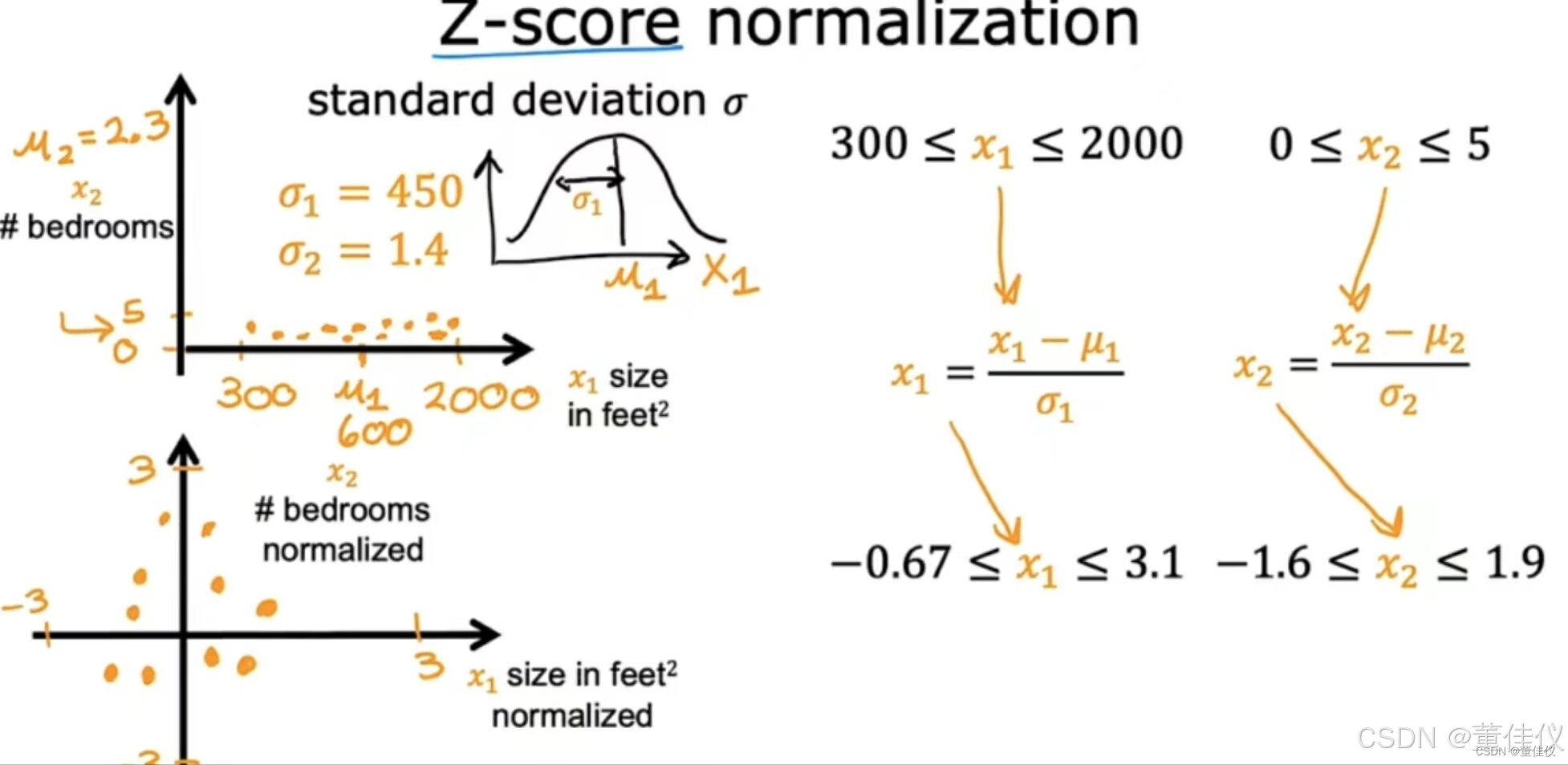 根据经验,在执行特征缩放时,你可能希望将功能范围从任何地方每个特征x大约为负一到大约加一。但是这些值,负一和正一可能有点松散。如果范围从负三到正三或负0.3到正0.3.所有这些都完全没问题。如果你有一个特征x_1最终介于0到3之间,这不是问题。如果你愿意,你可以重新缩放它,但如果你不重新缩放它,它也应该可以正常工作。或者,如果你有不同的特征x_2,其值介于负数之间2再加上0.5,其次,没关系,重新缩放它没有害处,但是,如果你也不管他,那也没事。但是如果另一个特征,比如这里的x_3,范围从负100到正100,那么这具有非常不同的值范围,例从负一到正一你可能最好重新放缩这个特性x_3所以他的范围从接近负一到正一。同样,如果你有一个特征x_4具有非常小的值,比如在-0.00001和正0.00001之间,那么这些值是如此之小这意味着你可能想重新缩放它。最后如果你的特征x_5例医院病人受体温范围从98.6-105华氏度在这种情况下这些值在100左右,实际上相当大与其他比例特征相比,这实际上会导致梯度下降运行更慢。在这种情况下,特征重新缩放可能会有所帮助。几乎没有任何伤害进行特征重新缩放。
根据经验,在执行特征缩放时,你可能希望将功能范围从任何地方每个特征x大约为负一到大约加一。但是这些值,负一和正一可能有点松散。如果范围从负三到正三或负0.3到正0.3.所有这些都完全没问题。如果你有一个特征x_1最终介于0到3之间,这不是问题。如果你愿意,你可以重新缩放它,但如果你不重新缩放它,它也应该可以正常工作。或者,如果你有不同的特征x_2,其值介于负数之间2再加上0.5,其次,没关系,重新缩放它没有害处,但是,如果你也不管他,那也没事。但是如果另一个特征,比如这里的x_3,范围从负100到正100,那么这具有非常不同的值范围,例从负一到正一你可能最好重新放缩这个特性x_3所以他的范围从接近负一到正一。同样,如果你有一个特征x_4具有非常小的值,比如在-0.00001和正0.00001之间,那么这些值是如此之小这意味着你可能想重新缩放它。最后如果你的特征x_5例医院病人受体温范围从98.6-105华氏度在这种情况下这些值在100左右,实际上相当大与其他比例特征相比,这实际上会导致梯度下降运行更慢。在这种情况下,特征重新缩放可能会有所帮助。几乎没有任何伤害进行特征重新缩放。 这就是特征缩放。有了这个技巧,你通常可以得到梯度下降运行得更快。
这就是特征缩放。有了这个技巧,你通常可以得到梯度下降运行得更快。

![[JAVAEE] 网络编程](https://i-blog.csdnimg.cn/direct/e202db1a84c741d3b3a086fedfbfdab4.png)