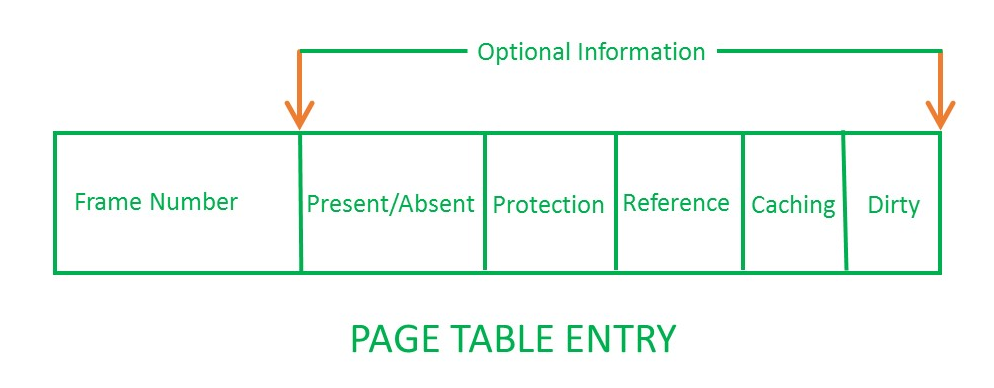
读书笔记:学习空间变换的三种数学表达形式。
文章目录
- 1. 旋转矩阵
- 1.1 向量运算
- 1.2 坐标系空间变换
- 1.3 变换矩阵与齐次坐标
- 2. 旋转向量和欧拉角
- 2.1 旋转向量
- 2.2 欧拉角
- 3. 四元数
1. 旋转矩阵
1.1 向量运算
对于三维空间中的两个向量 a , b ∈ R 3 a,b \in \R^3 a,b∈R3,其内积可描述向量间的投影关系, c o s < a , b > cos<a,b> cos<a,b>表示两向量的夹角:

外积:

外积运算结果为一个垂直于 a , b a,b a,b的向量,大小为 ∣ a ∣ ∣ b ∣ s i n < a , b > |a||b|sin<a,b> ∣a∣∣b∣sin<a,b>(两个向量组成的四边形的有向面积)。
对外积运算,引入符号^,把 a a a写成一个反对称矩阵(Skew-symmetric Matrix),这样就把外积变成线性运算。这是一个一一映射,即任意向量都对应唯一的一个反对称矩阵,反之亦然:
a ^ = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] a\hat{}= \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} a^= 0a3−a2−a30a1a2−a10
1.2 坐标系空间变换
包括旋转和平移两个过程,由矩阵 T T T 表示。
旋转过程由**旋转矩阵(Rotation Matrix)**表示,它是一个 3 × 3 3 \times 3 3×3的矩阵,且是一个行列式为1的正交矩阵(反之行列式为1的正交矩阵是一个旋转矩阵)。将n维旋转矩阵集合定义如下(特殊正交群(Special Orthogonal Group),后面讲):
S O ( n ) = { R ∈ R n × n ∣ R R T = 1 , d e t ( R ) = 1 } SO(n)=\{R \in \R^{n \times n} | RR^T=1, det(R)=1 \} SO(n)={R∈Rn×n∣RRT=1,det(R)=1}
平移过程由平移向量 t表示。
1.3 变换矩阵与齐次坐标
变换矩阵T(Transform Matrix)是一个 4 × 4 4 \times 4 4×4矩阵,由旋转矩阵R和平移向量t组成。可由特殊欧氏群表示这一集合:
S E ( 3 ) = { T = [ R t 0 T 1 ] ∈ R 4 × 4 ∣ R ∈ S O ( 3 ) , t ∈ R 3 } SE(3)=\{ T= \begin{bmatrix} R & t \\ 0^T & 1 \end{bmatrix} \in \R^{4 \times 4} | R \in SO(3), t \in \R^3 \} SE(3)={T=[R0Tt1]∈R4×4∣R∈SO(3),t∈R3}
T − 1 = [ R T − R T t 0 T 1 ] T^{-1} = \begin{bmatrix} R^T & -R^Tt \\ 0^T & 1 \end{bmatrix} T−1=[RT0T−RTt1]
对三维向量进行空间变换运算时,在其末尾添加1变成四维向量,便于运算,称为齐次坐标。
2. 旋转向量和欧拉角
利用矩阵表示旋转存在两个问题:
- SO(3)用9个量表示3个自由度的旋转、SE(3)用16个量表示6自由度的变换,不够紧凑;
- 旋转矩阵自身约束:必须正交、行列式为1,因此很难直接对其进行优化;
2.1 旋转向量
任意旋转都可以用一个旋转轴和一个旋转角来表示:具体可用一个向量来表示,其方向与旋转轴一致,而长度等于旋转角,这类向量称为旋转向量(或轴角/角轴,Axis-Angle),仅需一个三维向量即可描述旋转;
同样,可用一个旋转向量和一个平移向量来表达一次变换;
旋转矩阵R和旋转向量(旋转轴为单位向量n,角度为 θ \theta θ) 之间的转换过程由罗德里格斯公式推导:

反之可由旋转向量推导出旋转矩阵,具体推导过程参考原书和链接。
2.2 欧拉角
可由翻滚角Roll、偏航角Yaw和俯仰角Pitch表示。注意几个问题:
- 绕不同轴的旋转顺序会影响最终结果;
- 在很多工程应用领域,利用欧拉角表示旋转很容易碰到万向锁(Gimbal Lock) 问题;
3. 四元数
问题来源:
- 旋转矩阵用9个量描述3自由度的旋转,具有冗余性;
- 欧拉角和旋转向量时紧凑的,但具有奇异性(万向锁);
使用四元数可以很方便地对空间运动数据进行优化,一个四元数 q q q 由一个实部和三个虚部构成:
q = q 0 + q 1 i + q 2 j + q 3 k = [ s , v ] T s = q 0 ∈ R v = [ q 1 , q 2 , q 3 ] T ∈ R 3 q=q_0+q_1i+q_2j+q_3k=[s,v]^T \\ s=q_0 \in \R \\ v=[q_1,q_2,q_3]^T \in \R^3 q=q0+q1i+q2j+q3k=[s,v]Ts=q0∈Rv=[q1,q2,q3]T∈R3
这部分推导直接看书吧,没什么好总结的:
- 四元数的运算;
- 四元数表示旋转;
- 四元数转旋转矩阵、旋转向量;