前置知识
前置知识:极限
我们要求 lim x → 1 x 2 − 1 x − 1 \lim\limits_{x \to 1}\dfrac{x^2-1}{x-1} x→1limx−1x2−1。
右边我们都知道是什么意思,那左边是什么呢?
意思就是,当 x x x 无限接近 1 1 1 时,右边的那一坨东西是什么。
x x x 无限接近 1 1 1 是什么意思?管他呢,我们先直接代入 x = 1 x=1 x=1 求一下呗,然后求出来一个非常谔谔的 0 0 \dfrac{0}{0} 00。
然而当我们画出这个函数的图像后:
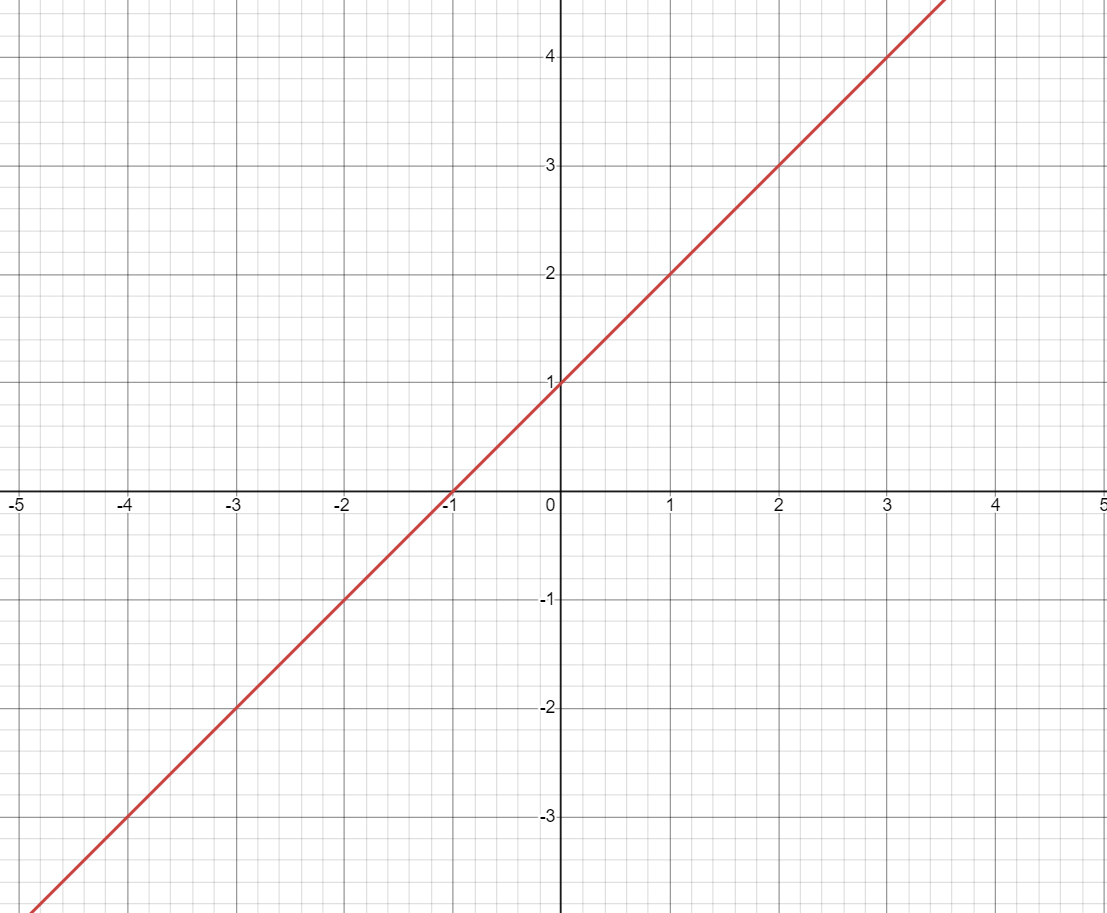
这不就是一个 x + 1 x+1 x+1 吗?太 easy 了,通过 瞪眼法 直觉可知,答案是 2 2 2。
有个东东叫做:验算。
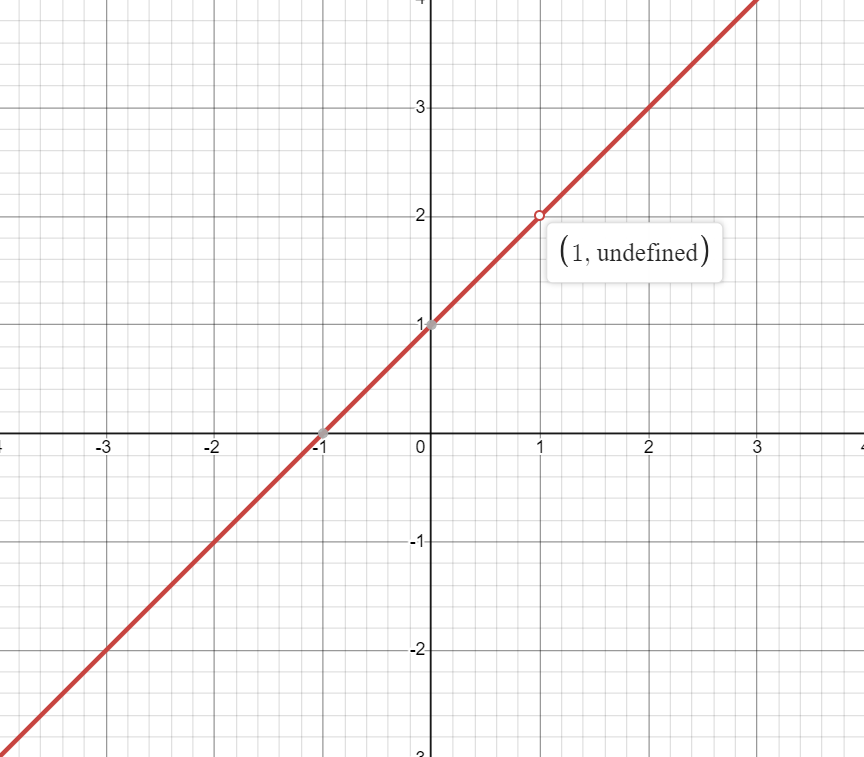
阿哲,难道答案就是“未定义”吗?
当你重新回去审视题面,你发现了被你直接遗忘掉的 lim x → 1 \lim\limits_{x \to 1} x→1lim。
也就是,漏掉了一句,当 x x x 无限接近 1 1 1 的时候,意味着 x x x 可以不是 1 1 1,也可以是 1 + 1 0 − 114514 1+10^{-114514} 1+10−114514 等。
-
当 x x x 取 2 2 2 时,原函数的值为 3 3 3。
-
当 x x x 取 1.5 1.5 1.5 时,原函数的值为 2.5 2.5 2.5。
-
当 x x x 取 1 + 1 0 − 114514 1+10^{-114514} 1+10−114514 时,原函数的值为 2 + 1 0 − 114514 2+10^{-114514} 2+10−114514。
-
当 x x x 取 1 − 1 0 − 114514 1-10^{-114514} 1−10−114514 时,原函数的值为 2 − 1 0 − 114514 2-10^{-114514} 2−10−114514。
其中,第三条和第四条的 x x x 都非常接近 1 1 1,而这四条的值都越来越接近 2 2 2。
综上,答案是 2 2 2。
相信通过这个例子都已经可以理解极限到底是个啥东东了,放一波百度百科对于极限的描述:
某一个函数中的某一个变量,此变量在变大(或者变小)的永远变化的过程中,逐渐向某一个确定的数值 A A A 不断地逼近而“永远不能够重合到 A A A”(“永远不能够等于 A A A,但是取等于 A A A‘已经足够取得高精度计算结果)的过程中,此变量的变化,被人为规定为“永远靠近而不停止”、其有一个“不断地极为靠近 A A A 点的趋势”。极限是一种“变化状态”的描述。此变量永远趋近的值 A A A 叫做“极限值”(当然也可以用其他符号表示)。
update:一点小小的补充
有一写特别的函数,其在某一点处的值存在然而极限不存在。
极限的严格定义是,左极限和右极限相等才算有。
而左极限就是从左边无限逼近,右极限就是从右边无限逼近。
比如这个经典的分段函数:
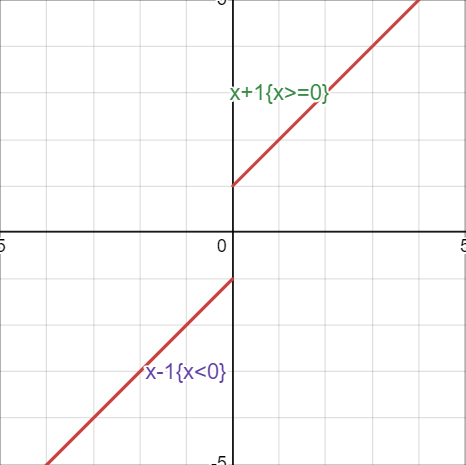
注意上面是当 x ≥ 0 x \ge 0 x≥0 时取的 x + 1 x+1 x+1,而下面是 x < 0 x<0 x<0,所以当 x = 0 x=0 x=0 时有定义,是 1 1 1。
而 x = 0 x=0 x=0 时的左极限是 − 1 -1 −1,你从左边无限逼近就是 − 1 -1 −1,右极限是 1 1 1,左右极限并不相等,所以极限不存在,但是值存在(为 1 1 1)。
前置知识:导数
其实就是斜率。
但是,测量斜率要有一条直线,也就是两个点。
比如,我们要测量下图中直线 g 1 g_1 g1 和 g 2 g_2 g2 的斜率:
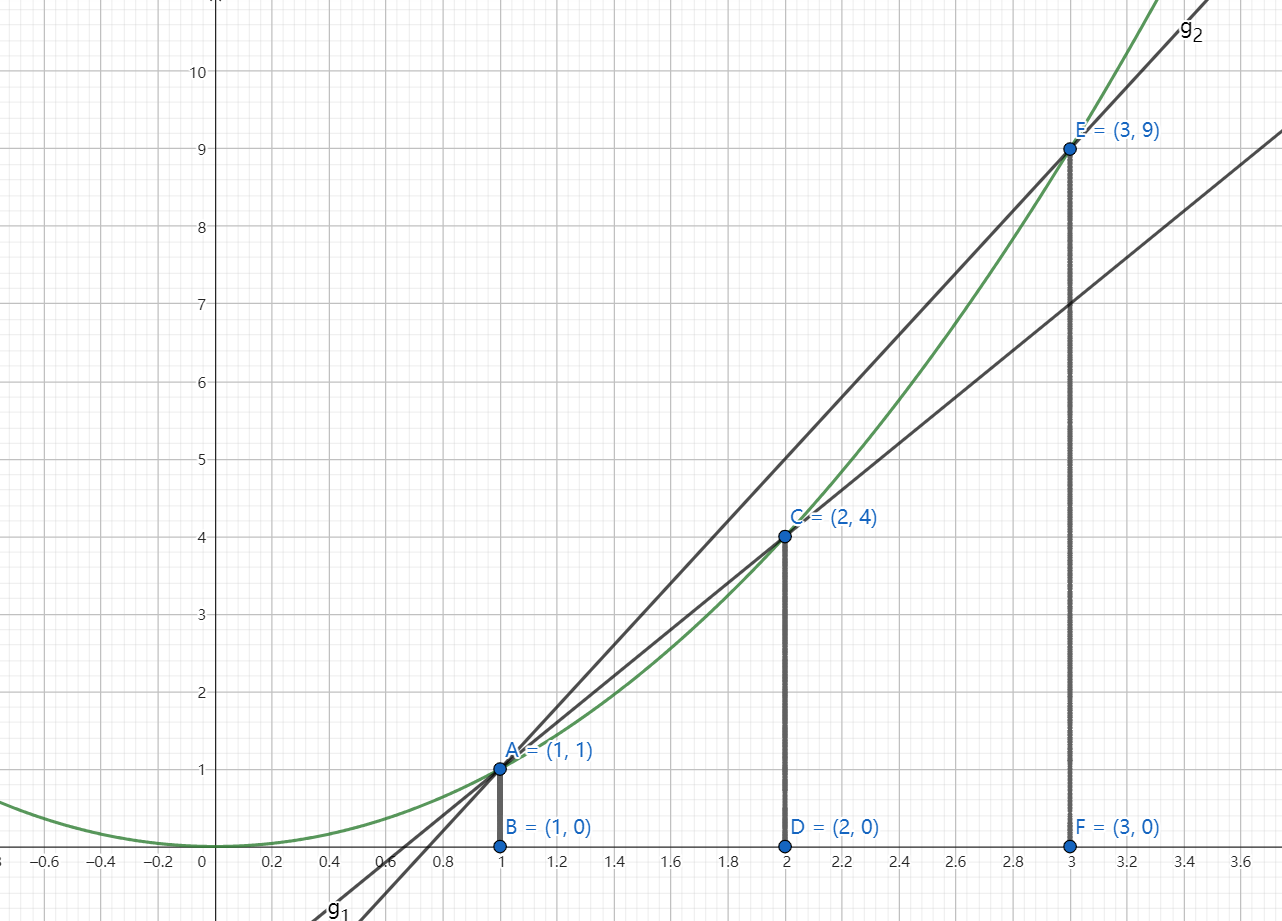
根据斜率公式, Δ y Δ x \dfrac{\Delta y}{\Delta x} ΔxΔy 也就是 y 2 − y 1 x 2 − x 1 \dfrac{y_2-y_1}{x_2-x_1} x2−x1y2−y1,可以求出直线 g 1 g_1 g1 的斜率为 4 − 1 2 − 1 = 3 \dfrac{4-1}{2-1} = 3 2−14−1=3, g 2 g_2 g2 的斜率是 9 − 1 3 − 1 = 4 \dfrac{9-1}{3-1} = 4 3−19−1=4。
那么,如果我们只有一个在一个函数图像上的点,我们应该如何求出斜率呢?
有人说,你这样不行啊!一个点怎么可能可以求斜率呢?
update:对,你说的没错,一个点不能求斜率,这里的斜率实际上指的是过这个点的函数图像的 切线 的斜率。
但是,我们可以取一个在这个函数的图像上,和这个点非常相近的点,比如要求斜率的点是在 f ( x ) = x 2 f(x)=x^2 f(x)=x2 上的 x = 1 x=1 x=1 点,那么我们可以取一个 x = 1.01 x=1.01 x=1.01 点,这样求出来的斜率是:
f ( 1.01 ) − f ( 1 ) 1.01 − 1 = 1.0 1 2 − 1 2 0.01 = 0.0201 0.01 = 2.01 \begin{aligned} \frac{f(1.01)-f(1)}{1.01-1} &= \frac{1.01^2-1^2}{0.01} \\ &= \frac{0.0201}{0.01} \\ &= 2.01\end{aligned} 1.01−1f(1.01)−f(1)=0.011.012−12=0.010.0201=2.01
那么如果我们取的第二个点就是原来的点呢?
f ( 1 ) − f ( 1 ) 1 − 1 = 0 0 \frac{f(1)-f(1)}{1-1} = \frac{0}{0} 1−1f(1)−f(1)=00
分母变成 0 0 0 了!
当然,我们可以再写一个函数,设 g ( x ) g(x) g(x) 为“与 1 1 1 相邻的那个点”选择 x x x 时算出来的斜率。
我们可以直接通过斜率公式求得:
g ( x ) = x 2 − 1 x − 1 g(x) = \frac{x^2-1}{x-1} g(x)=x−1x2−1
看上去没什么用,但是如果你学了多项式除法,或者学了一点点小学奥数,那么就会知道 x 2 − 1 = ( x − 1 ) ( x + 1 ) x^2-1 = (x-1)(x+1) x2−1=(x−1)(x+1),原式就相当于 x + 1 x+1 x+1。
然后我们就发现,当 x = 1 x=1 x=1 时可以求 g ( x ) g(x) g(x) 了!求出来就是 1 + 1 = 2 1+1=2 1+1=2。所以在 f ( x ) = x 2 f(x)=x^2 f(x)=x2 函数上的 x = 1 x=1 x=1 点的斜率就是 2 2 2。
然后,我们就可以扩大一下 g ( x ) g(x) g(x),使其变成 g ( x , y ) g(x,y) g(x,y),意思是“与 y y y 相邻的那个点”选择 x x x 时算出来的斜率。
g ( x , y ) = x 2 − y 2 x − y g(x,y)=\frac{x^2-y^2}{x-y} g(x,y)=x−yx2−y2
(上面的 g g g 函数只是 y = 1 y=1 y=1 时的特化)
一样的道理, x 2 − y 2 = ( x − y ) ( x + y ) x^2-y^2=(x-y)(x+y) x2−y2=(x−y)(x+y),那么 g ( x , y ) g(x,y) g(x,y) 就相当于 x + y x+y x+y,然后我们一样就发现 g ( y , y ) g(y,y) g(y,y) 也能求出来了,就相当于 y + y = 2 y y+y=2y y+y=2y。
既然 g ( y , y ) g(y,y) g(y,y) 也可以求出来了,那肯定就是最精确的。那我们干嘛还去求其他的呢?所以我们再用一个函数 f ′ ( x ) f'(x) f′(x) 来代表在 f ( x ) f(x) f(x) 上 x x x 点的斜率,同时可以轻松得到, f ′ ( x ) = g ( x , x ) = 2 x f'(x)=g(x,x)=2x f′(x)=g(x,x)=2x。
我们就称 f ′ ( x ) f'(x) f′(x) 为 f ( x ) f(x) f(x) 的导函数,其意义就是 f ( x ) f(x) f(x) 的图像上 x x x 点的斜率。
最后放一波百度百科对于导数的描述:
导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数 y = f ( x ) y=f(x) y=f(x) 的自变量 x x x 在一点 x 0 x_0 x0 上产生一个增量 Δ x \Delta x Δx 时,函数输出值的增量 Δ y \Delta y Δy 与自变量增量 Δ x \Delta x Δx 的比值在 Δ x \Delta x Δx 趋于 0 0 0 时的极限 a a a 如果存在, a a a 即为在 x 0 x_0 x0 处的导数,记作 f ′ ( x 0 ) f'(x_0) f′(x0) 或 d f ( x 0 ) d x \dfrac{df(x_0)}{dx} dxdf(x0)。
当然,除了上面两种,极限还有第三种表达方式: d d x f ( x 0 ) \dfrac{d}{dx}f(x_0) dxdf(x0)。
需要注意的是, d d x \dfrac{d}{dx} dxd 并不能约分变成 1 x \dfrac{1}{x} x1, d d d 是一个非常特殊的量,叫做无穷小,如果不理解可以在前面加上 lim d → 0 \lim\limits_{d \to 0} d→0lim,当然我们现在并不需要理解它的意思。
嗯,其实导数还有另外一种定义:
f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x f'(x)=\lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x)-f(x)}{\Delta x} f′(x)=Δx→0limΔxf(x+Δx)−f(x)
我们来解析一下:
f ′ ( x ) f'(x) f′(x) 代表导数。
lim Δ x → 0 \lim\limits_{\Delta x \to 0} Δx→0lim 代表 Δ x \Delta x Δx,也就是 x x x 的增量尽量小。
f ( x + Δ x ) − f ( x ) Δ x \dfrac{f(x + \Delta x)-f(x)}{\Delta x} Δxf(x+Δx)−f(x) 下面的 Δ x \Delta x Δx 可以变成 ( x + Δ x ) − x (x + \Delta x) - x (x+Δx)−x 可能会更好理解,你会发现其实还是在求斜率。
其实意思就是:选一个与 x x x 尽量靠近(靠近到不能在靠近)的数字,对其求值作为另一个点,对于原来的 x x x 点和选取的与 x x x 尽量靠近做的直线的点求斜率。
前置知识:原函数
反导数,一个函数 f f f 的原函数通常记作 F F F,满足 F ′ ( x ) = f ( x ) F'(x)=f(x) F′(x)=f(x)。
积分
这是一个标准的正弦函数:
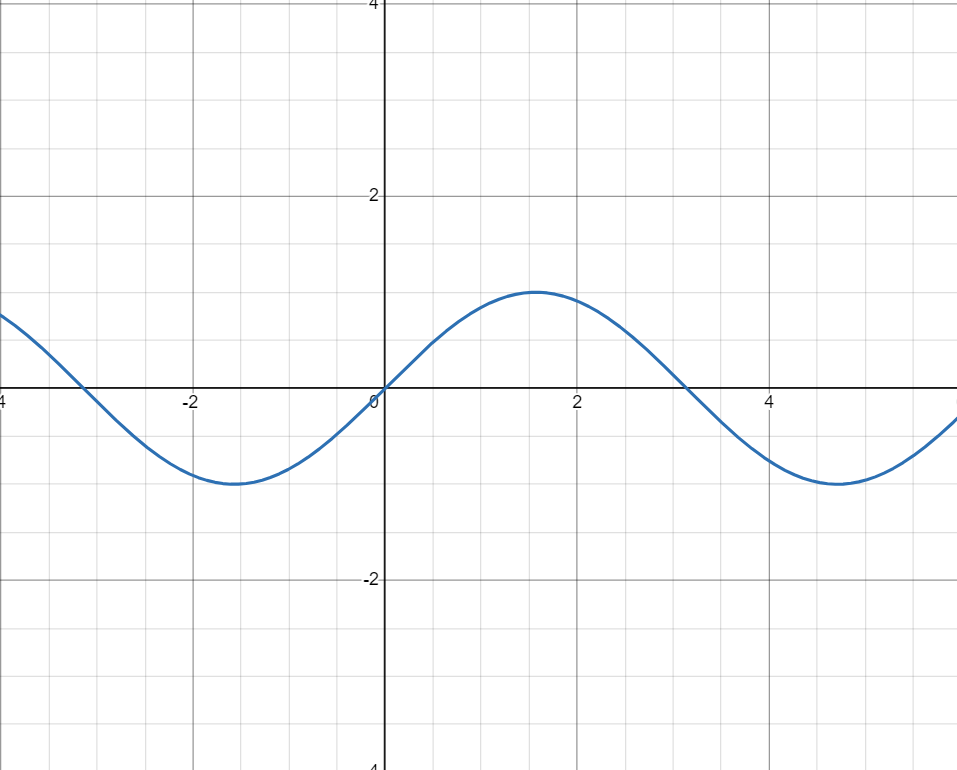
它很简单(并不),这时,几何老师来了:
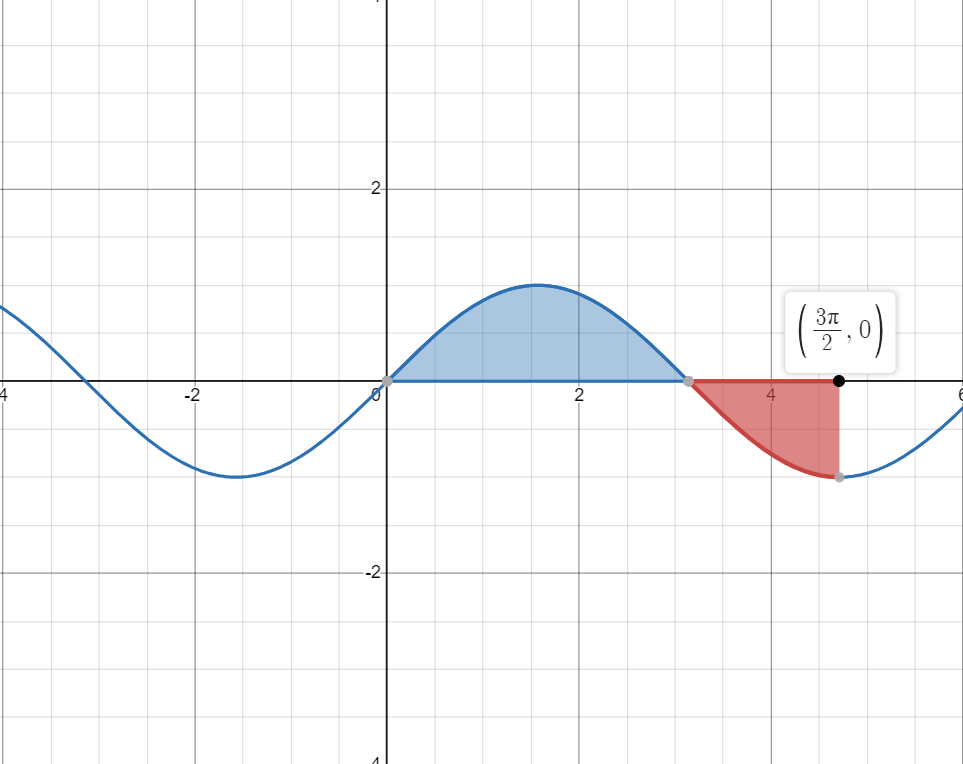
『求阴影部分面积。』(蓝色是正的,红色是负的。)
其实可以这样求,把阴影部分看做是若干个长方形的面积之和。
比如:
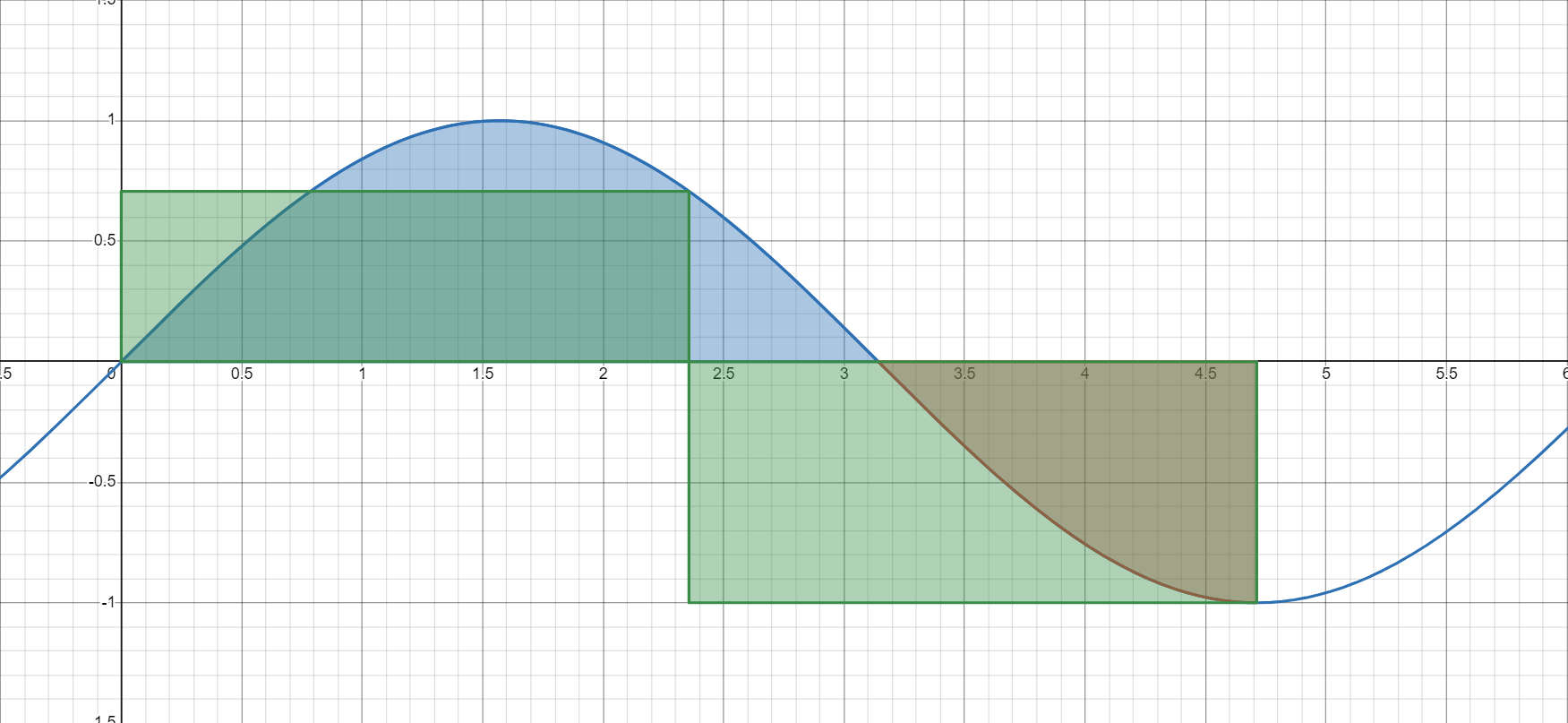
这样显然不太精确,可以这样:

还可以这样:
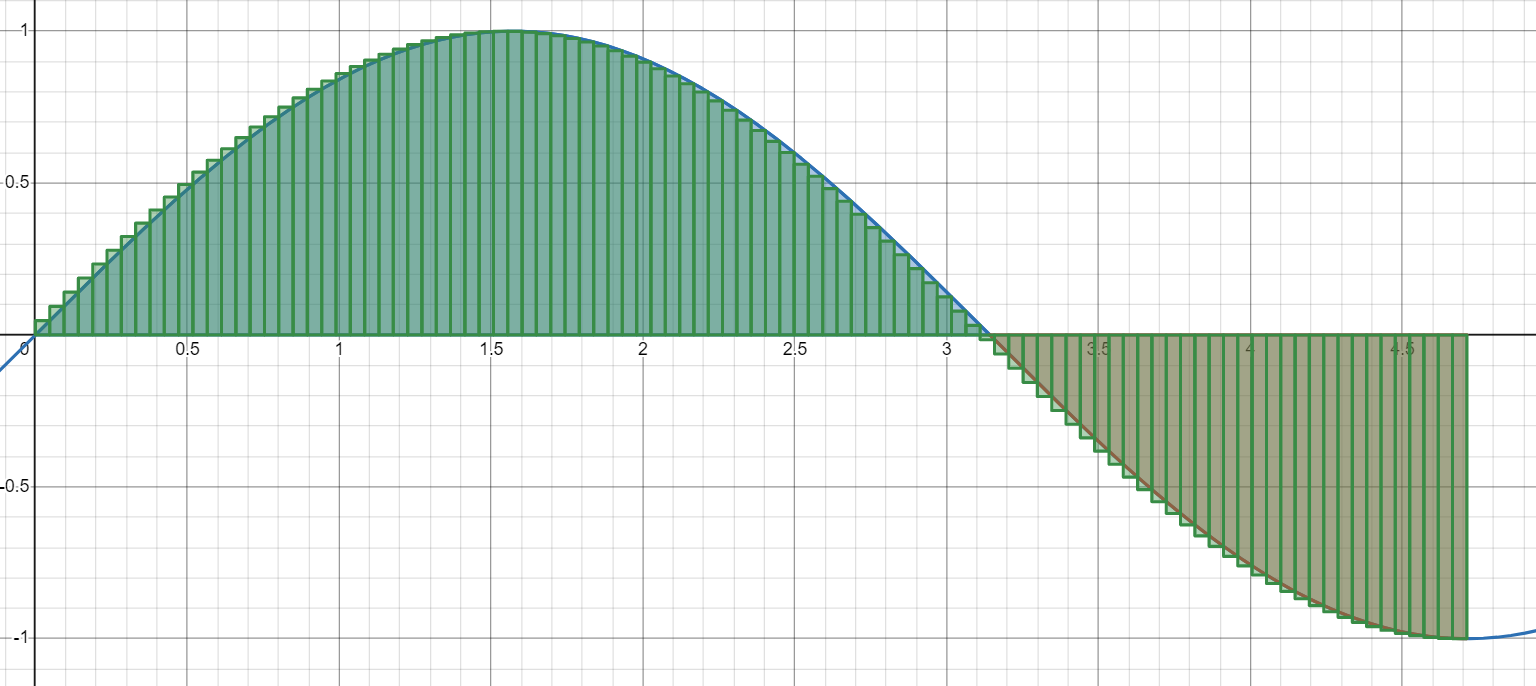
甚至这样:
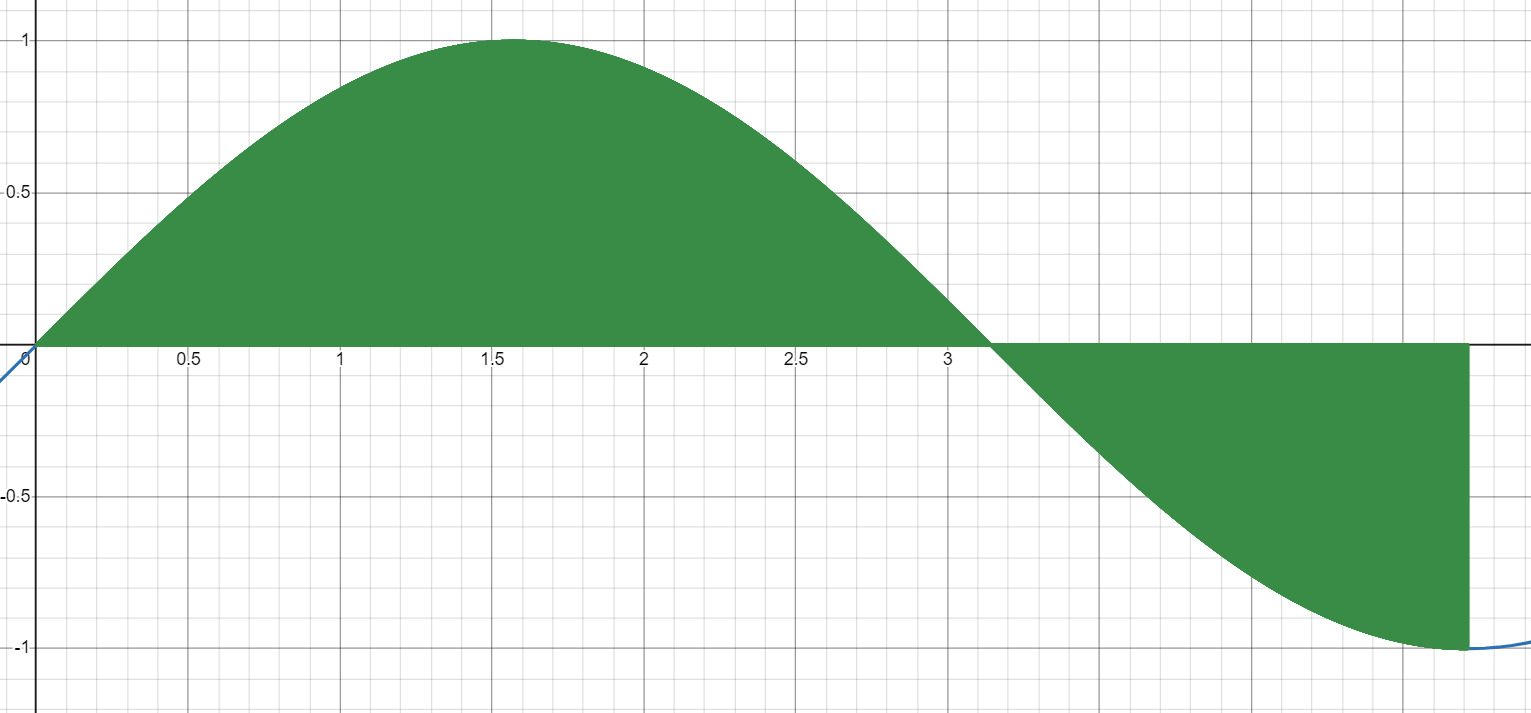
显然,最后一张图已经基本上是正确答案了,肉眼看不出区别。
如果我们用数学方法求呢?
那就是:
lim d x → 0 ∑ i = 0 d x ( 3 π 2 ) d x sin ( d x i ) d x \lim\limits_{\mathrm dx \to 0} \sum_{i={0 \over \mathrm dx}}^{({3\pi \over 2}) \over \mathrm dx} \sin(\mathrm dxi)\mathrm dx dx→0limi=dx0∑dx(23π)sin(dxi)dx
但是,这种 $ \lim\limits_{\mathrm dx \to 0} \sum \limits_{i={a \over \mathrm dx}}^{b \over \mathrm dx} f(\mathrm dxi)\mathrm dx $ 形式的式子在微积分里面太常见了,所以简记做 $ \int _a^b f(x)\mathrm dx $。
换句话说,我们要求 ∫ 0 3 π 2 sin ( x ) d x \int_0^{3\pi \over 2}\sin(x)\mathrm dx ∫023πsin(x)dx。
特别厉害的注意力
我们要求 $ \int _a^b f’(x)\mathrm dx $。
而 f ′ ( x ) f'(x) f′(x) 就是 lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x \lim\limits_{\Delta x \to 0} \frac{f(x + \Delta x)-f(x)}{\Delta x} Δx→0limΔxf(x+Δx)−f(x)。
然而这里 Δ x \Delta x Δx 和 d x \mathrm dx dx 都是趋近于 0 0 0 的,可以合并在一起。
那么原式就是:
∫ a b f ( x + d x ) − f ( x ) d x d x \int _a^b \frac{f(x + \mathrm dx)-f(x)}{\mathrm dx}\mathrm dx ∫abdxf(x+dx)−f(x)dx
也就是:
∫ a b f ( x + d x ) − f ( x ) \int _a^b f(x+\mathrm dx)-f(x) ∫abf(x+dx)−f(x)
我们发现这是一个差分的前缀和,所答案就是:
f ( b ) − f ( a ) f(b)-f(a) f(b)−f(a)
综上:
∫ a b f ′ ( x ) d x = f ( b ) − f ( a ) \int_a^b f'(x)\mathrm dx = f(b)-f(a) ∫abf′(x)dx=f(b)−f(a)
也就是:
∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_a^b f(x)\mathrm dx = F(b)-F(a) ∫abf(x)dx=F(b)−F(a)
恭喜你,你发现了微积分基本定理,也就是牛顿 - 莱布尼茨公式!
这样,我们就能解这道题了。
$ \sin x $ 的原函数是 − cos x -\cos x −cosx,所以答案就是 ( − cos 3 π 2 ) − ( − cos 0 ) = 0 − ( − 1 ) = 1 (-\cos \frac{3\pi}{2}) - (-\cos 0) = 0 - (-1) = 1 (−cos23π)−(−cos0)=0−(−1)=1。
这就是求定积分的简单方法:微积分基本定理,但是前提是这个函数你能求出它的原函数。
其实计算机对于一般的函数求积分还是分成极小的小块。
比如:
>>> from math import *
>>> def f(x):
... return sin(x)
...
>>> def myint(f, a, b, dx): #对于 f 函数求 a 到 b 的定积分,长方形的宽为 dx
... sum = 0
... for i in range(int(a / dx),int(b / dx)):
... sum += dx * f(i * dx)
... return sum
>>> myint(f, 0, 3*pi/2, 1/1)
1.8918884196934453
>>> myint(f, 0, 3*pi/2, 1/10)
1.06154102847852
>>> myint(f, 0, 3*pi/2, 1/100)
1.0073806105888143
>>> myint(f, 0, 3*pi/2, 1/1000)
1.0008888969713063
>>> myint(f, 0, 3*pi/2, 1/1000000) #过了许久
1.0000014803845385
看到没,其实还是挺精确的,并且许多微分方程(通俗来就就是求原函数,或者多阶原函数)都是无解的,只能通过计算机模拟。