前言

我们模型的控制方程，即浅水方程组的表达式如下：
$$\begin{gathered} \frac{\partial \mathbf{U}}{\partial t}+\frac{\partial \mathbf{E}(\mathbf{U})}{\partial x}+\frac{\partial \mathbf{G}(\mathbf{U})}{\partial y}=\mathbf{S}(\mathbf{U}) \\ \mathbf{U}=\left(\begin{array}{c}h\\ hu\\ hv\end{array}\right),\mathbf{E}(\mathbf{U})=\left(\begin{array}{c}hu\\ h{u}^2+\frac{g{h}^2}{2}\\ huv\end{array}\right),\mathbf{G}(\mathbf{U})=\left(\begin{array}{c}hv\\ huv\\ h{v}^2+\frac{g{h}^2}{2}\end{array}\right), \\ \mathbf{S}(\mathbf{U})=\left(\begin{array}{c}0\\ gh(S_{0x}-S_{fx})\\ gh(S_{0y}-S_{fy})\end{array}\right) \\ {S}_{0x}=-\frac{\partial z_b}{\partial x},S_{0y}=-\frac{\partial z_b}{\partial y} \\ {S}_{fx}=n^{2}u\sqrt{u^2+v^2}{h}^{-4/3},S_{fy}=n^{2}v\sqrt{u^2+v^2}{h}^{-4/3} \end{gathered}$$
对此，我们首先将式中物理量离散于三角形网格中，后采用有限体积法将浅水方程改写成其离散形式。在离散的浅水方程中，水位、流速等物理量的计算可转化为对网格界面的通量项和网格内源项的计算。对于离散方程中的通量项，本模型将会采用基于Riemann近似解的Roe格式数值求解界面通量。

基于有限体积法的方程离散

对于我们的浅水模型，水深、流速等物理量被定义在网格中心，如下图所示。对于网格i与j，它们间的质量、动量传输是通过其网格边界E_i,j发生的（下图中加粗的网格边）。网格i和j之间边界的外法相量定义为n=(n_x, n_y)。

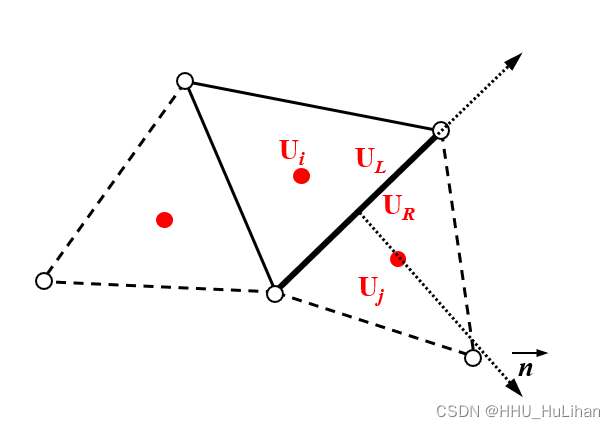
之后，对于控制体网格i，我们采用高斯散度定理将浅水方程沿着边界E_i,j线积分，得到：
$${\iint }_{\Omega }\frac{\partial \mathbf{U}}{\partial t}d\Omega =-{\int }_S[\mathbf{E}(\mathbf{U})n_x+\mathbf{G}(\mathbf{U})n_y]ds+{\iint }_{\Omega }\mathbf{S}(\mathbf{U})d\Omega$$
式中，Ω表示网格i所对应的控制体，S表示边界E_i,j；dΩ和ds分别表示面积分和线积分的微元。

在我们的模型中，各个水力要素在网格体内被假定是均匀分布的。在对上式的时间导数项采用前差格式离散，得到数值解为：
$$\begin{gathered} {\mathbf{U}}_i^{n+1}={\mathbf{U}}_i^n-\frac{\Delta t}{{\Omega }_i}\sum _{j=1}^3{\mathbf{F}}_{nj}{L}_j+\Delta t\bar{S} \\ {\mathbf{F}}_{\mathbf{n}}=\mathbf{E}(\mathbf{U})n_x+\mathbf{G}(\mathbf{U})n_y \end{gathered}$$
其中，Δt为时间步长，Ω_i表示网格单元i的面积，F_nj表示网格i中第j条边的外通量，L_j表示网格i中第j条边的长度；S表示源项，$\bar{S}$表示源项S在网格i的体积分值。

注意，上式就是模型求解过程中最核心的表达式。它完成了从该时间步水力变量到下一步水力变量的更新计算。

界面通量与源项计算

接下来要解决的问题是通量项${\mathbf{F}}_{\mathbf{n}}$的计算。首先，我们将网格边通量计算转化为一个Riemann近似解问题。采用Roe格式来求解这个近似黎曼解：
$${\mathbf{F}}_{\mathbf{n}}=\frac{1}{2}(\mathbf{E}({\tilde{\mathbf{U}}}_{\mathbf{L}})+\mathbf{G}({\tilde{\mathbf{U}}}_{\mathbf{R}}))-\sum _{k=1}^3{\tilde{\alpha }}^k|{\lambda }^k|{\gamma }^k)$$
式中， ${\lambda }^k$为基于 Roe 平均的雅克比矩阵$J$的特征值， ${\gamma }^k$为特征值对应的特征向量；${\alpha }^k$表示特征强度。各项表达如下：
$$\{\begin{array}{rl}{\lambda }^1& =\tilde{u}-\tilde{c}\\ {\lambda }^2& =\tilde{u}\\ {\lambda }^3& =\tilde{u}+\tilde{c}\end{array},\{\begin{array}{rl}{\gamma }^1& =(1,u-\tilde{c},\tilde{v}{)}^T\\ {\gamma }^2& =(0,0,1{)}^T\\ {\gamma }^3& =(1,u+\tilde{c},\tilde{v}{)}^T\end{array},\{\begin{array}{rl}{\tilde{\alpha }}^1& =\frac{1}{2}[h_R-h_L-\frac{\tilde{h}}{\tilde{c}}(u_R-u_L)]\\ {\tilde{\alpha }}^2& =\tilde{h}(v_R-v_L)\\ {\tilde{\alpha }}^3& =\frac{1}{2}[h_R-h_L+\frac{\tilde{h}}{\tilde{c}}(u_R-u_L)]\end{array}$$
上述变量中下标L和R分别表示该变量是边界内、外侧网格上的值（如上图所示）；$\tilde{u}$、$\tilde{v}$、$\tilde{c}$和$\tilde{h}$都是Roe平均变量，定义如下：
$$\begin{gathered} \tilde{u}=\frac{u_L\sqrt{h_L}+u_R\sqrt{h_R}}{\sqrt{h_L}+\sqrt{h_R}},\tilde{v}=\frac{v_L\sqrt{h_L}+v_R\sqrt{h_R}}{\sqrt{h_L}+\sqrt{h_R}}, \\ \tilde{c}=\sqrt{\frac{g(h_L+h_R)}{2}},\tilde{h}=\sqrt{h_L{h}_R} \end{gathered}$$
注意，此处下标含L和R的速度$\tilde{u}$均是垂直于网格边（与外法向n同向）的速度分量，且波速c的方向也与外法向n同向。同理，下标含L和R的$\tilde{v}$则是与法相量n相垂直。

此外，对源项S中的底坡和摩阻项的处理将直接关系到模型的计算精度和稳定性。为了获得和谐、守恒的结果，对底坡源项进行特征分解和迎风处理以适应Riemann求解格式。首先，对底坡源项在控制体Ω内积分得到${\bar{S}}_0$：
$$\begin{gathered} {\bar{S}}_0=\sum _{j=0}^3\sum _{k=0}^3[\frac{1}{2}(1-sign(\overline{{\lambda }^k}))({\beta }^k\overline{r^k})L_j{]}^j \\ ({\beta }^1,{\beta }^2,{\beta }^3)=(-\frac{1}{2}\tilde{c}\Delta z_b,0,\frac{1}{2}\tilde{c}\Delta z_b),\Delta z_b=(z_b{)}_L-(z_b{)}_R \\ \overline{r^1}=\left(\begin{array}{c}1\\ \tilde{u}+\tilde{c}\\ \tilde{v}\end{array}\right),\overline{r^2}=\left(\begin{array}{c}0\\ 0\\ \tilde{c}\end{array}\right),\overline{r^3}=\left(\begin{array}{c}1\\ \tilde{u}-\tilde{c}\\ \tilde{v}\end{array}\right), \end{gathered}$$
式中，sign( )为符号函数。

为增加格式的稳定性，对摩阻源项进行半隐式离散，其表达式为：
$${\mathbf{S}}_f=(1-\theta ){\mathbf{S}}_f^n+\theta {\mathbf{S}}_f^{n+1}={\mathbf{S}}_f^n+\theta \frac{\partial {\mathbf{S}}_f}{\partial \mathbf{U}}\frac{\partial \mathbf{U}}{\partial t}\Delta t$$
θ=0时意味着完全显式，θ=1时意味着完全隐式；令${\mathbf{Q}}_f=\frac{\partial {\mathbf{S}}_f}{\partial \mathbf{U}}$，离散后的动量方程通量表达式为：
$$\Delta \mathbf{U}={\mathbf{U}}^{n+1}-{\mathbf{U}}^n=[\mathbf{I}-\Delta t\theta {\mathbf{Q}}_f^n{]}^{-1}[\frac{\Delta t}{{\Omega }_i}\sum _{j=1}^3({\mathbf{F}}_{nj}+\sum _{k=0}^3[\frac{1}{2}(1-sign(\overline{{\lambda }^k}))({\beta }^k\overline{r^k}))L_j+\Delta t{\mathbf{S}}_f]$$

干-湿网格的处理

对于复杂的地形，计算区域内的实际模拟范围和计算边界变化频繁。网格上可能出现淹没-干底-再淹没的过程，这对模型的计算提出较高的稳定性要求。为避免水深较小时网格=出现流速过大的非物理现象，本模型采用限制水深法来准确、稳定地模拟网格淹没、干底这一过程。
首先，设置两个临界水深$h_{dry}$和$h_{wet}$（且$h_{dry}<h_{wet}$），再将网格分为三类：

1. 当水深大于$h_{wet}$，该网格为“湿网格”，参与正常的模拟计算，同时求解质量和动量通量；
2. 当水深小于$h_{dry}$，该网格为“干网格”，不参与当前时间步的计算；
3. 当水深在$h_{dry}$和$h_{wet}$之间，该网格为“半干网格”，仅计算该时间步的质量通量，而没有计算动量通量。

数值离散的稳定性条件

本模型基于Riemann显式方法，即当前时刻的网格变量可直接由上一时刻的计算结果得到，无需经过迭代计算。但显式求解法受到CFL条件的限制，实际计算过程中的最大时间步长通常不为定值。
本模型将采用动态时间步长方法得到模拟的时间步长；同时需要用户输入一个可允许的最大步长$\Delta t_{max}$，以及一个允许的最大Courant数$C_{max}$($0<C<1.0$)。模型的时间步长按下式确定：
$$\Delta t=min(\Delta t_{max},C_{max}min(\frac{R_i}{\sqrt{u_i^2+v_i^2}+\sqrt{g{h}_i}})),i=1,2,3,...,N_c$$

参考文献

1. 刘臻,史宏达,黄燕.一种基于Roe格式的有限体积法在二维溃坝问题中的应用[J].中国海洋大学学报：自然科学版, 2007, 37(2):5.
2. [王志力,耿艳芬,金生.具有复杂计算域和地形的二维浅水流动数值模拟[J].水利学报, 2005, 36(4):6.