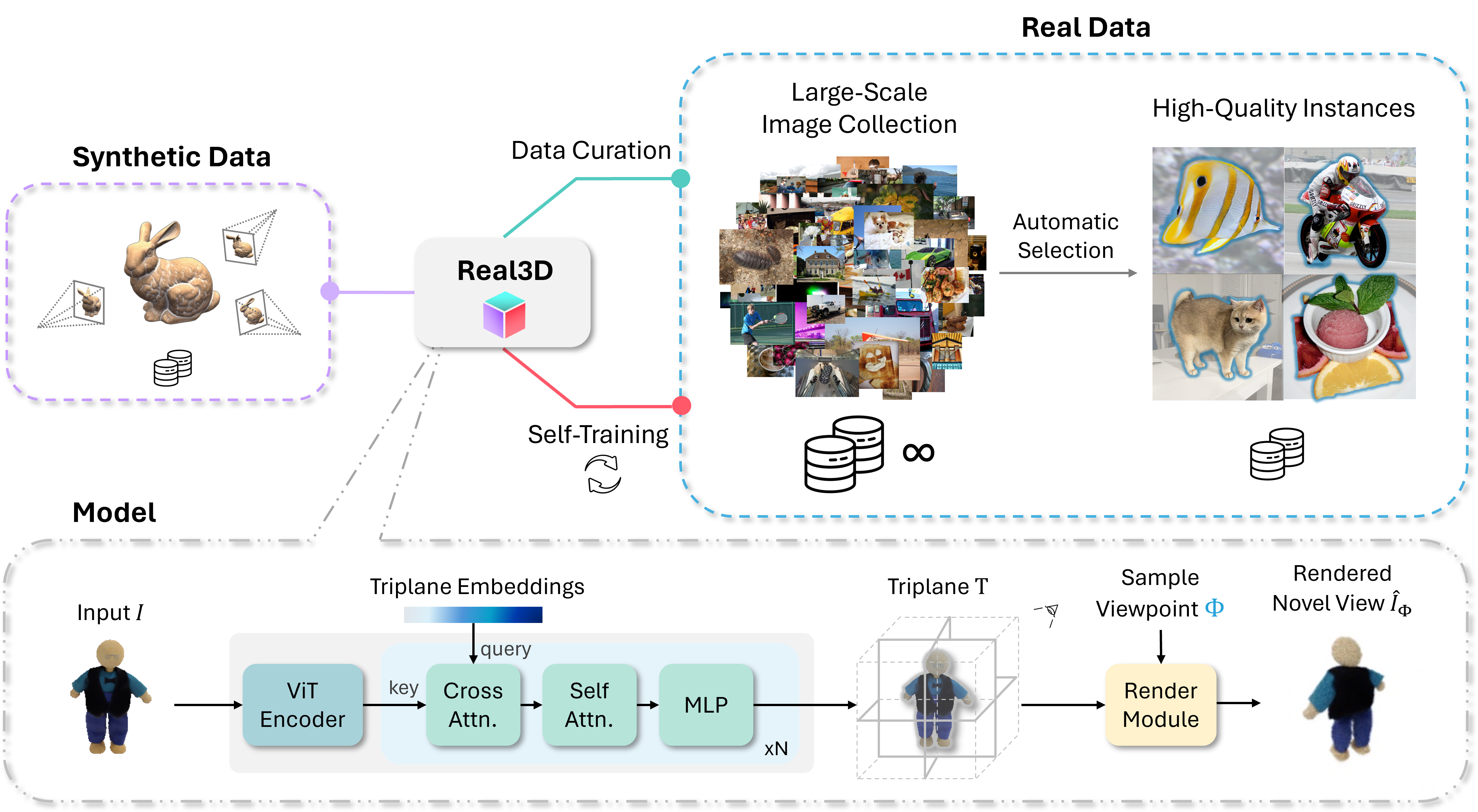
前馈神经网络又叫全连接神经网络、多层感知器，在网络中信息由输入到输出单向传递，具体特点有：

• 个神经元分别属于不同的层，层内无连接
• 相邻两层之间的神经元全部两两连接
• 整个网络中无反馈，信号从输入层像输出层单向传播，可用一个有向无环图表示
  

之后内容中的符号解释

其中，网络层数$L$、神经元个数$M_l$、激活函数$f_l(\cdot )$是超参数。于是，前馈神经网络可以通过下面公式进行信息传播：
$$\begin{array}{rl}& z^{(l)}=W^{(l)}{a}^{(l-1)}+b^{(l)}\\ & a^{(l)}=f_l(z^{(l)})\end{array}\}\Rightarrow a^{(l)}=f_l(W^{(l)}{a}^{(l-1)}+b^{(l)})$$
一层中的每一个神经元都是上一层所有神经元的加权汇总，$f_l(z^{(l)})$是按元素的激活函数（对向量中的每个元素分别带入计算）
整个前馈计算：
$$x=a^0\to z^{(1)}\to a^{(1)}\to z^{(2)}\to \cdots \to a^{(L-1)}\to z^{(L)}\to a^{(L)}=\varphi (x;w,b)$$
上一层的输出a经过加权汇总（$Wa+b$）得到本层输入z，输入z经过激活函数得到本层输出a，依次类推。

通用近似定理

• “挤压”性质的激活函数：当输入值域较大时，其输出在两端时饱和的，具有S型函数曲线以及压缩输入值域的作用¹。例如Logistic函数和tanh函数（Sigmoid函数）。
  通用近似定理是说对于一个无论多么复杂的函数$f(x)$总能找到一个的函数$F(x)$来近似表示。也就是说，理论上神经网络只要隐藏层数量足够，可以近似解决任何连续函数能够表示的问题²。
  举个例子，一个前馈神经网络可以记为$w^2\sigma (w^{1}x+b^1)+b^2$，该网络具有线性输出层$w^{2}x+b^2$，隐藏层$\sigma (w^{1}x+b^1)$，且隐藏层中包含具有挤压性质的激活函数，那么对于该网络来说，只要隐藏层数量足够多，该神经网络可以近似实数空间中任意一个有界闭集函数。
  但实际上对与具有两层或多层的任意函数（不具有挤压性质）构成隐藏层的前馈网络来说，该结论仍然成立（因为通用近似定理本来是作为Sigmoid函数的一种性质提出的²）。也就是说，任意组合多个函数（不管是S型函数还是斜坡函数还是复合函数）最后都可以实现某种复杂的非线性映射。

应用到机器学习

神经网络可以作为一个“万能”函数来使用，可以用来进行复杂特征转换，或逼近一个复杂的条件分布。
$$\hat{y}=\underset{分类器}{\underbrace{g(\stackrel{神经网络}{\overbrace{\varphi (x)}};\theta )}}$$
如果分类器为Logistic回归分类器或者Softmax回归分类器（目前已经接触到的分类器有：Logistic分类器、Softmax分类器、感知器、SVM，后面俩个属于单独的神经网络结构，不应该与其他混为一谈），那么分类器也可以看作是神经网络的最后一层（输出层），这样神经网络输出的活性值就直接对应不同类别的条件概率，即$P(y|x)=\varphi (x)$。同样的，Logistic和Softmax回归也可以看作是只有一层的神经网络。
以多分类问题 y ∈ { 1 , ⋯ , C } y\in\{1,\cdots,C\} y∈{1,⋯,C}为例，采用Softmax回归分类器，输出层为第L层，共需要设置C个神经元分别输出某个分类的条件概率（C维one-hot向量）
$$\begin{array}{rl}& z^{(L)}=\varphi (x)\\ & \hat{y}=\mathrm{softmax}(z^{(L)})\end{array}$$
其中$z^{(L)}$是第L层的输入，这里将softmax看作激活函数。
然后采用交叉熵损失函数
$$\mathcal{L}(y,\hat{y})=-y^T\log \hat{y}$$
对于训练集$D=\{(x^{(n)},y^{(n)}){\}}_{n=1}^N$，输入样本$x^{(n)}$输出预测条件概率${\hat{y}}^{(n)}$，取结构化风险函数（学习准则）为：
$$\mathcal{R}(W,b)=\frac{1}{N}\sum _{n=1}^N\mathcal{L}(y^{(n)},{\hat{y}}^{(n)})+\frac{1}{2}\lambda \Vert W{\Vert }_F^2$$
其中正则化项采用Frobenius范数，即$\Vert W{\Vert }_F^2={\sum }_{l=1}^L{\sum }_{i=1}^{M_i}{\sum }_{j=1}^{M_{i-1}}(w_{ij}^{(l)}{)}^2$，意思是求所有参数$w$的平方和（第$l$个样本在神经网络第$i$层中第$j$个神经元的参数）

损失函数：评估模型单次预测好坏
风险函数：度量平均意义下模型的好坏

然后进行梯度下降，计算风险函数对于每一层参数（$W^{(l)}$和$b^{(l)}$）的梯度，
$$\begin{array}{r}\frac{\partial \mathcal{R}(W,b)}{\partial W^{(l)}}\\ \frac{\partial \mathcal{R}(W,b)}{\partial b^{(l)}}\end{array}$$
由于神经网络是复合函数，计算时可利用求导数的链式法则

但实际上并不需要像这样一个一个对梯度进行计算，可以用反向传播算法或自动微分的方法来计算风险函数的梯度。
最后朝梯度反方向对参数进行更新即可。

---

1. 08.1 挤压型激活函数 - AI-EDU (microsoft.github.io) ↩︎

2. 通用近似定理（学习笔记）-CSDN博客 ↩︎ ↩︎