---

引言

隔了好长时间没看概率论了，上一篇文章还是 8.29 ，快一个月了。主要是想着高数做到多元微分和二重积分题目，再来看这个概率论二维的来，更好理解。不过没想到内容太多了，到现在也只到二元微分的进度。

---

一、二维随机变量及分布

1.1 基本概念

定义 1 —— 二维随机变量。设 $X,Y$ 为定义于同一样本空间上的两个随机变量，称 $(X,Y)$ 为二维随机变量。同理，也有 $n$ 维随机变量的定义。

定义 2 —— 二维随机变量的分布函数。

（1）设 $(X,Y)$ 为二维随机变量，对任意的 $x,y\in R$ ，称 F ( x , y ) = P { X ≤ x , Y ≤ y } F(x,y)=P\{X\leq x,Y\leq y\} F(x,y)=P{X≤x,Y≤y} 为二维随机变量 $(X,Y)$ 的联合分布函数。

（2）称函数 F X ( x ) = P { X ≤ x } , F Y ( y ) = P { Y ≤ y } F_X(x)=P\{X\leq x\},F_Y(y)=P\{Y\leq y\} FX​(x)=P{X≤x},FY​(y)=P{Y≤y} 分别为随机变量 $X,Y$ 的边缘分布函数。同理，有 $n$ 维随机变量的联合分布函数以及边缘分布函数。

1.2 联合分布函数的性质

设 $(X,Y)$ 为二维随机变量，$F(x,y)$ 为其联合分布函数，有如下性质：

（1）$0\le F(x,y)\le 1;$

（2）$F(x,y)$ 对 $x,y$ 都是单调不减函数；

（3）$F(x)$ 关于 $x,y$ 都是右连续；

（4）$F(-\infty ,-\infty )=0=F(-\infty ,+\infty )=F(+\infty ,-\infty )=0,F(+\infty ,+\infty )=1.$

其实和一维随机变量的分布函数的性质大差不差的，我也是从一维那里复制过来改了下的hhh。

以下是一些推论：

（1）设 { X ≤ x } = A , { Y ≤ y } = B \{X\leq x\}=A,\{Y\leq y\}=B {X≤x}=A,{Y≤y}=B ，则 $F(x,y)=P(AB),F_X(x)=P(A),F_Y(y)=P(B).$ 即联合分布函数是要取交集。

（2）$F_X(x)=F(x,+\infty ),F_Y(y)=F(+\infty ,y).$ 即当一个变量限制在小于正无穷范围（这是肯定的），当然此时联合分布函数和边缘分布函数一致了。

（3）设 $a_1<a_2,b_1<b_2$ ，则

P { a 1 < X ≤ a 2 , b 1 < Y ≤ b 2 } = P { a 1 < X ≤ a 2 , Y ≤ b 2 } − P { a 1 < X ≤ a 2 , Y ≤ b 1 } = ( P { X ≤ a 2 , Y ≤ b 2 } − P { X ≤ a 1 , Y ≤ b 2 } ) − ( P { X ≤ a 2 , Y ≤ b 1 } − P { X ≤ a 1 , Y ≤ b 1 } ) = F ( a 2 , b 2 ) − F ( a 1 , b 2 ) − F ( a 2 , b 1 ) + F ( a 1 , b 1 ) . P\{a_1 < X\leq a_2,b_1 < Y \leq b_2\}=P\{a_1 < X\leq a_2,Y\leq b_2\}-P\{a_1 < X\leq a_2,Y \leq b_1\}=(P\{X \leq a_2,Y\leq b_2\}-P\{X \leq a_1,Y\leq b_2\})-(P\{X \leq a_2,Y\leq b_1\}-P\{X\leq a_1,Y\leq b_1\})=\pmb{F(a_2,b_2)-F(a_1,b_2)-F(a_2,b_1)+F(a_1,b_1)}. P{a1​<X≤a2​,b1​<Y≤b2​}=P{a1​<X≤a2​,Y≤b2​}−P{a1​<X≤a2​,Y≤b1​}=(P{X≤a2​,Y≤b2​}−P{X≤a1​,Y≤b2​})−(P{X≤a2​,Y≤b1​}−P{X≤a1​,Y≤b1​})=F(a2​,b2​)−F(a1​,b2​)−F(a2​,b1​)+F(a1​,b1​).

---

二、二维离散型随机变量及分布

设 $(X,Y)$ 为二维随机变量，若 $(X,Y)$ 的可能取值为有限对或可列对，称 $(X,Y)$ 为二维离散型随机变量。

设随机变量 $(X,Y)$ 的可能取值为 $(x_i,y_j)(i=1,2,\cdots ,m;j=1,2,\cdots ,n)$ ，称 P { X ≤ x i , Y ≤ y j } = p i j ( i = 1 , 2 , ⋯ , m ; j = 1 , 2 , ⋯ , n ) , 或 P\{X\leq x_i,Y\leq y_j\}=p_{ij}(i=1,2,\cdots,m;j=1,2,\cdots,n),或 P{X≤xi​,Y≤yj​}=pij​(i=1,2,⋯,m;j=1,2,⋯,n),或

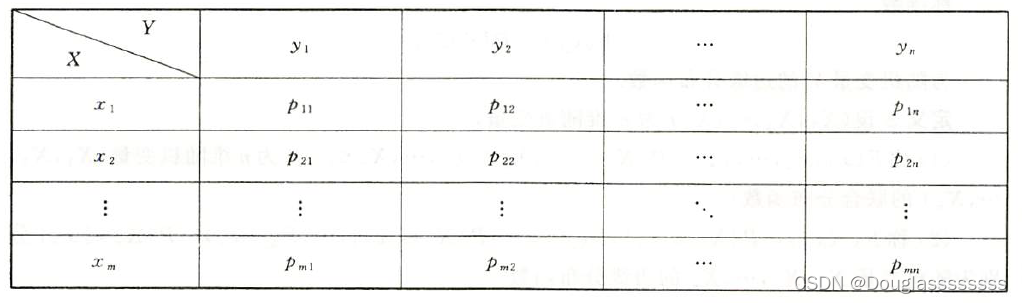
为 $(X,Y)$ 的联合分布律。其具有如下性质：

1. $p_{ij}\ge 0(i=1,2,\cdots ,m;j=1,2,\cdots ,n);$
2. $\sum \sum p_{ij}=1.$

由全概率公式，有 P { X = x i } = P { X = x i , y 1 } + ⋯ + P { X = x i , y n } = p i 1 + ⋯ + p i , n = p i ( i = 1 , 2 , ⋯ , m ) . P\{X=x_i\}=P\{X=x_i,y_1\}+\cdots+P\{X=x_i,y_n\}=p_{i1}+\cdots+p_{i,n}=p_i(i=1,2,\cdots,m). P{X=xi​}=P{X=xi​,y1​}+⋯+P{X=xi​,yn​}=pi1​+⋯+pi,n​=pi​(i=1,2,⋯,m). 同理，可以得到 P { Y = y i } P\{Y= y_i\} P{Y=yi​} 。于是，联合分布律每一行每一列之和，即可构成两个随机变量的边缘分布律。

一般情况下，联合分布律和边缘分布律可以放在一张表格中：

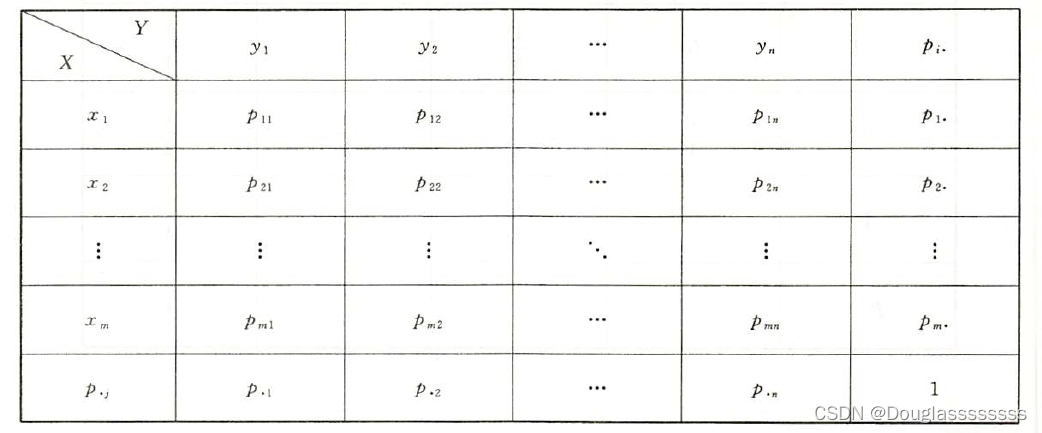
三、多维连续型随机变量及分布

3.1 基本概念

设 $(X,Y)$ 为二维随机变量，其分布函数为 F ( x , y ) = P { X ≤ x , Y ≤ y } F(x,y)=P\{X\leq x,Y\leq y\} F(x,y)=P{X≤x,Y≤y} ，若存在非负可积函数 $f(x,y)$ ，使得 $F(x,y)={\int }_{-\infty }^{x}du{\int }_{-\infty }^{y}f(u,v)dv$ ，称 $(X,Y)$ 为二维连续型随机变量，$f(x,y)$ 为 $(X,Y)$ 的联合密度函数，$F(x,y)$ 为联合分布函数。

称 $f_X(x)={\int }_{-\infty }^{\infty }f(x,y)dy,f_Y(y)={\int }_{-\infty }^{\infty }f(x,y)dx$ 分别为随机变量 $X,Y$ 的边缘密度函数。

称 $F_X(x)={\int }_{-\infty }^x{f}_X(x)dx,F_Y(y)={\int }_{-\infty }^y{f}_Y(y)dy$ 分别为随机变量 $X,Y$ 的边缘分布函数。

同理，以上结论可推广到 $n$ 维。

3.2 二维连续型随机变量的性质

设 $f(x,y)$ 为二维随机变量 $(X,Y)$ 的联合密度函数，则

1. $f(x,y)\ge 0;$
2. ${\int }_{-\infty }^{\infty }dx{\int }_{-\infty }^{\infty }f(x,y)dy=1.$

设 $(X,Y)$ 为二维连续型随机变量，$f(x,y)$ 为其联合密度函数，$F(x,y)$ 为其联合分布函数。若 $F(x,y)$ 在某点 $(x,y)$ 处二阶可偏导，有 $$f(x,y)=\frac{\partial F}{\partial x\partial y};$$ 若在某点处二阶不可偏导，则 $f(x,y)=0$ 。

二阶联合分布函数一定连续，但不一定二阶可偏导。

---

写在最后

果然，先去看看多元微分和多重积分，看这个就较为轻松。