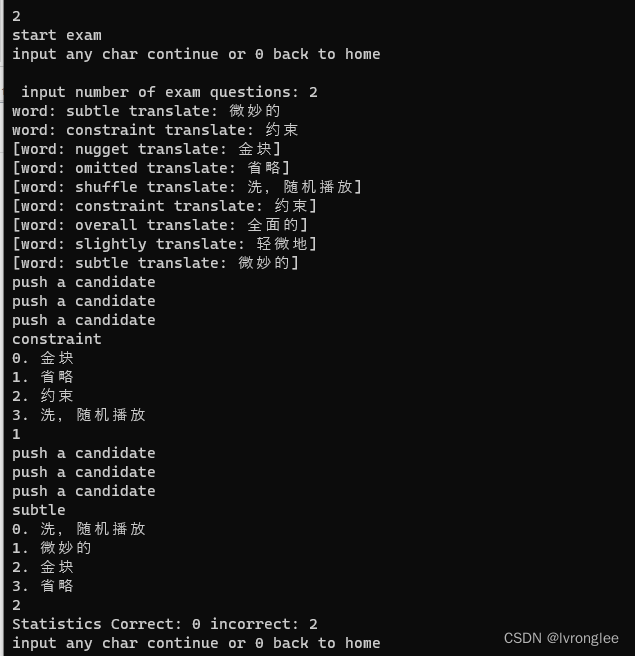
使用非线性优化方法求解ICP

---

欢迎访问个人网络日志🌹🌹知行空间🌹🌹

---

前情提要

在迭代最近点算法ICP及SVD求解中介绍了ICP问题及使用SVD分解求解ICP的方法。除了SVD，还可以使用非线性优化的方法来求解ICP。

ICP问题回顾

还记得，ICP优化的目标函数为：

$$\underset{R,t}{\min }\frac{1}{2}\sum _i^n||p_i-(R{q}_i+t)|{|}_2^2$$

我们知道旋转和平移可以写成齐次变换的形式，

$$T=\left[\begin{array}{cc}R& t\\ 0& 0\end{array}\right]$$

ICP优化的目标函数可以写成：

$$\underset{T}{\min }\frac{1}{2}\sum _i^n||p_i-T{q}_i|{|}_2^2$$

这里要优化的变量是$T$，而$T$是矩阵？如何对矩阵求导数呢？需要使用李群与李代数的概念。

对矩阵变量求导数

根据《视觉SLAM十四讲》第4讲的介绍，$T$属于特殊欧式群$SE(3)$，$SE(3)$具有连续性质，是李群。

李群局部正切空间上的表示是李代数，李代数相对于李群，类似于导数对函数的意义。

$SE(3)$对应的李代数$se(3)$为：

$$se(3)=\left\{\xi =\left[\begin{array}{c}\rho \\ \varphi \end{array}\right]\in {\mathbb{R}}^6,\rho \in {\mathbb{R}}^3,\varphi \in so(3),{\xi }^{\wedge }=\left[\begin{array}{cc}{\varphi }^{\wedge }& \rho \\ 0^T& 0\end{array}\right]\in {\mathbb{R}}^{4\times 4}\right\}$$

其中，$\xi$是$se(3)$的元素,是包含平移$\rho$和旋转$\varphi$的六维向量。$\varphi$其实是$so(3)$的元素。

$\wedge$符号这里表示将六维向量转换成四维矩阵。

在$t=0$附近，齐次变换矩阵可以由$T=exp({\xi }_{0}t)$计算出来，由此可以看到，齐次变换矩阵与一个反对称矩阵${\xi }_0^{\wedge }t$建立了联系，在一时刻对于给定的$T$,可以求得一个$\xi$,其描述了$T$在局部的导数关系。

矩阵的指数运算显然没有定义，如何计算呢？这里可以用泰勒公式，

$$exp(A)=\sum _{n=0}^{\infty }\frac{1}{n!}{A}^n$$

将$\xi$写成旋转加平移的形式$[\rho ,\varphi {]}^T$,再将$\varphi$写成模长和方向的形式$\varphi =\theta a$,代入上面的公式可得：

$$exp({\xi }^{\wedge })=\left[\begin{array}{cc}\sum _{n=0}^{\infty }\frac{1}{n!}({\varphi }^{\wedge }{)}^n& \sum _{n=0}^{\infty }\frac{1}{(n+1)!}({\varphi }^{\wedge }{)}^n\rho \\ 0& 1\end{array}\right]\triangleq \left[\begin{array}{cc}R& J\rho \\ 0^T& 1\end{array}\right]=T$$

当$\varphi =\theta a$时，推导可得

$$J=\frac{sin\theta }{\theta }I+(1-\frac{sin\theta }{\theta })a{a}^T+\frac{1-cos\theta }{\theta }{a}^{\wedge }$$

当在李群中完成两个矩阵的乘法时，也就是依次进行两个变换时，李代数上对应会发生怎样的变化呢？

$SE(3)$是$se(3)$的指数映射，那么

$exp({\xi }_1^{\wedge })exp({\xi }_2^{\wedge })$是否等于$exp(({\xi }_1+{\xi }_2{)}^{\wedge })$呢？对于矩阵的指数运算，上式并不成立。

两个李代数指数映射乘积的完整形式，由Baker-Campbell-Hausdorff(BCH)公式给出，

$ln(exp(A)exp(B))=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+...$

[,]是李括号，表示二元运算。

以旋转矩阵组成的特殊正交群$SO(3)$为例，

考虑$SO(3)$上的李代数$(ln(exp({\varphi }_1^{\wedge })({\varphi }_2^{\wedge })){)}^{\wedge }$,当${\varphi }_1$或${\varphi }_2$为小量，BCH公式中李括号二次以上的项可以忽略掉，则可得近似线性表示为，

$$(ln(exp({\varphi }_1^{\wedge })({\varphi }_2^{\wedge })){)}^{\vee }\approx \{\begin{array}{cc}{J}_l({\varphi }_2{)}^{-1}{\varphi }_1+{\varphi }_2& {\varphi }_1为小量\\ J_r({\varphi }_1{)}^{-1}{\varphi }_2+{\varphi }_1& {\varphi }_2为小量\end{array}$$

上面公式中第一种相当于是对原旋转矩阵左乘一个微小变换矩阵，第二种相当于是对原旋转矩阵右乘一个微小变换矩阵。乘以微小变换矩阵相当于是发生了微小的位移和姿态变化。

左乘微小变换矩阵的近似雅可比矩阵$J_l$同推导$se(3)$的指数映射中作用在平移向量$\rho$上的雅可比$J$

$$J_l=J=\frac{sin\theta }{\theta }I+(1-\frac{sin\theta }{\theta })a{a}^T+\frac{1-cos\theta }{\theta }{a}^{\wedge }$$。

通过上面的推导就建立了李群乘法和李代数加法之间的关系。

以旋转矩阵为例，对某个旋转$R$,其对应的李代数为$\varphi$,对其左乘一个微小旋转$△R$,其对应的李代数为$△\varphi$。那么在李群上的变化就为$△RR$,而对应的在李代数的变化根据BCH公式近似就为$J_l^{-1}(\varphi )△\varphi +\varphi$,综合以上可以写成：

$$exp(△{\varphi }^{\wedge })exp({\varphi }^{\wedge })=exp((\varphi +J_l^{-1}(\varphi )△\varphi ))$$

上面公式中，如果左乘的微小旋转矩阵对应的李代数带雅可比矩阵，则上式就变为(以左乘为例)：

$$exp((J_l(\varphi )△\varphi {)}^{\wedge })exp({\varphi }^{\wedge })=exp((\varphi +J_l^{-1}(\varphi )J_l(\varphi )△\varphi {)}^{\wedge })=exp((\varphi +△\varphi {)}^{\wedge })$$

由上，李代数上的加法，可近似为李群上带左或右雅可比的乘法：

$$exp((\varphi +△\varphi {)}^{\wedge })=exp((J_l(\varphi )△\varphi {)}^{\wedge })exp({\varphi }^{\wedge })=exp({\varphi }^{\wedge })exp((J_r(\varphi )△\varphi {)}^{\wedge })$$

因为旋转矩阵组成的李群各个变换之间只定义了有意义的乘法而没有定义有意义的加法，因此不能直接在李群上定义导数。

而考虑李群与李代数之间的关系，以旋转矩阵为例对$SO(3)$上的李代数求导，

$$\frac{\partial RP}{\partial R}$$

由于$SO(3)$上只对乘法满足封闭性，因此不能按照常规的微分定义来求导，设$R$对应的李代数为$\varphi$,由$R=exp({\varphi }^{\wedge })$可得

$$\begin{array}{rl}\frac{\partial exp({\varphi }^{\wedge })P}{\partial \varphi }& =\underset{\delta \varphi \to 0}{\lim }\frac{exp((\varphi +\delta \varphi {)}^{\wedge })p-exp({\varphi }^{\wedge })p}{\delta \varphi }\\ & =\underset{\delta \varphi \to 0}{\lim }\frac{exp(J_l(\varphi )\delta \varphi {)}^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\delta \varphi }\\ & =\underset{\delta \varphi \to 0}{\lim }\frac{(I+(J_l(\varphi )\delta \varphi {)}^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\delta \varphi }\\ & =\underset{\delta \varphi \to 0}{\lim }\frac{(J_l(\varphi )\delta \varphi {)}^{\wedge }exp({\varphi }^{\wedge })p}{\delta \varphi }\\ & =\underset{\delta \varphi \to 0}{\lim }\frac{-(exp({\varphi }^{\wedge })p{)}^{\wedge }{J}_l(\varphi )\delta \varphi }{\delta \varphi }\\ & =-(Rp{)}^{\wedge }{J}_l(\varphi )\end{array}$$

上面推导过程中1到2用到了BCH近似公式，2到3用到了泰勒公式，4到5用到了反对称矩阵的性质$A=-A^T$，最终得到了旋转后的点相对于旋转矩阵李代数的导数。

通过转换成李代数求导得到的最终的导数包含一个$J_l$矩阵，其形式和计算过于复杂。另外一种李群求导的方法是扰动模型，对$R$进行一个左乘或右乘扰动，将结果相对于扰动的变化率作为导数，以左乘扰动$△R$为例，其对应的李代数为$\phi$，推导如下：

$$\frac{\partial Rp}{\partial R}=\underset{\phi \to 0}{\lim }\frac{exp({\phi }^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\phi }$$

该式的求导可写成，

$$\begin{array}{rl}\frac{\partial Rp}{\partial R}& =\underset{\phi \to 0}{\lim }\frac{exp({\phi }^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{(I+{\phi }^{\wedge })exp({\varphi }^{\wedge })p-exp({\varphi }^{\wedge })p}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{{\phi }^{\wedge }Rp}{\phi }=\underset{\phi \to 0}{\lim }\frac{-(Rp{)}^{\wedge }\phi }{\phi }=-(Rp{)}^{\wedge }\end{array}$$

相比于对李代数直接求导，省去了一个雅可比$J_l$的计算。

ICP问题的非线性解法

考虑前面ICP优化的目标函数：

$$e=\underset{T}{\min }\frac{1}{2}\sum _i^n||p_i-T{q}_i|{|}_2^2=\underset{\xi }{\min }\frac{1}{2}\sum _{i=1}^n||(p_i-exp({\xi }^{\wedge })q_i)|{|}_2^2$$

$\xi$是$SE(3)$ $T$对应的李代数。

单个误差项关于位姿的导数，使用李代数的扰动模型可得，

$$\frac{\partial e}{\partial \xi }=\underset{\delta \xi \to 0}{\lim }\frac{e(\delta \xi \oplus \xi )-e(\xi )}{\delta \xi }$$

$\oplus$表示左乘模型

对于n对三维空间中的点$p$及其投影$q$,希望计算的相机旋转和平移分别为$R,t$其对应的李群为$T$。对于空间中的一点$p_i=[X_i,Y_i,Z_i{]}^T$，其对应的投影点像素坐标为${\mu }_i=[{\mu }_i,v_i{]}^T$,根据相机模型，有以下关系，

$$s_i\left[\begin{array}{c}{\mu }_i\\ v_i\\ 1\end{array}\right]=KT\left[\begin{array}{c}{X}_i\\ Y_i\\ Z_i\\ 1\end{array}\right]$$

写成矩阵的形式为：

$$s_i{\mu }_i=KT{p}_i$$

上式隐含了一次齐次坐标往三维坐标的转换。

对于n对空间点和对应的图像中投影的观测点，要估计相机的位姿，目标函数就是最小化两者之间的误差，

$$T^{\ast }=arg\underset{T}{\min }\frac{1}{2}\sum _{i=1}^n||{\mu }_i-\frac{1}{s_i}KT{p}_i||$$

记通过相机外参变换到相机坐标系下$p$点对应的点$q$的坐标为$q=(Tp{)}_{1:3}=[X^{\prime },Y^{\prime },Z^{\prime }]$

根据相机模型关于$q$点有：

$$s\mu =Kq$$

展开有：

$$\left[\begin{array}{c}s\mu \\ sv\\ s\end{array}\right]=\left[\begin{array}{ccc}{f}_x& 0& c_x\\ o& f_y& c_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{X}^{\prime }\\ Y^{\prime }\\ Z^{\prime }\end{array}\right]$$

重投影误差的左乘扰动求导数为：

$$\frac{\partial e}{\partial \xi }=\frac{\partial e}{\partial q}\frac{\partial q}{\partial \xi }$$

根据目标函数和相机模型的公式有：

$$\frac{\partial e}{\partial q}=-\left[\begin{array}{ccc}\frac{\partial \mu }{\partial X^{\prime }}& \frac{\partial \mu }{\partial Y^{\prime }}& \frac{\partial \mu }{\partial Z^{\prime }}\\ \frac{\partial v}{\partial X^{\prime }}& \frac{\partial v}{\partial Y^{\prime }}& \frac{\partial v}{\partial Z^{\prime }}\end{array}\right]=-\left[\begin{array}{ccc}\frac{f_x}{Z^{\prime }}& 0& -\frac{f_x{X}^{\prime }}{Z^{\prime 2}}\\ 0& \frac{f_y}{Z^{\prime }}& -\frac{f_y{Y}^{\prime }}{Z^{\prime 2}}\end{array}\right]$$

而第二项为变换后的点关于李代数的导数，

$$\frac{\partial (Tp)}{\partial T}=\left[\begin{array}{cc}I& -q^{\wedge }\\ 0& 0\end{array}\right]$$

根据$q$定义取出前三维，

$$\frac{\partial q}{\partial T}=[I,-q^{\wedge }{]}^T$$

最后将两者相乘可以求得$\frac{\partial e}{\partial \xi }$。

代码示例

使用G2O求解非线性优化问题，节点就是待求解变量，边是观测数据点。

前面推导的是相机模型的点与三维空间点的PnP问题的求解，对于ICP直接是成对三维点之间的优化，相对于PnP更简单。

定义G2O的顶点和边，

    class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;// 设置初始化的更新值 virtual void setToOriginImpl() override { _estimate = Sophus::SE3d();}// left multiplication on SE3virtual void oplusImpl(const double *update) {Eigen::Matrix<double, 6, 1> update_eigen;update_eigen << update[0], update[1], update[2],update[3], update[4], update[5];_estimate = Sophus::SE3d::exp(update_eigen) * _estimate;}virtual bool read(std::istream &in) override {return true;} virtual bool write(std::ostream &out) const override { return true;}};class EdgeProjectXYZRGBDPoseOnly : public g2o::BaseUnaryEdge<3, Eigen::Vector3d, bcv::VertexPose> {public:EIGEN_MAKE_ALIGNED_OPERATOR_NEW;EdgeProjectXYZRGBDPoseOnly(const Eigen::Vector3d &point) : _point(point) {}virtual void computeError() override {const VertexPose* p = static_cast<const VertexPose*> (_vertices[0]);_error = _measurement - p->estimate() * _point;}virtual void linearizeOplus() override {VertexPose *p = static_cast<VertexPose*> (_vertices[0]);Sophus::SE3d T = p->estimate();Eigen::Vector3d xyz_trans = T * _point;_jacobianOplusXi.block<3, 3>(0, 0) = -Eigen::Matrix3d::Identity();_jacobianOplusXi.block<3, 3>(0, 3) = Sophus::SO3d::hat(xyz_trans);}bool read(std::istream &in) { return true; }bool write(std::ostream &out) const { return true; }protected:Eigen::Vector3d _point;};

定义求解器：

    void ICPSolver::NLOSolver(std::vector<cv::Point3f> &pts1,std::vector<cv::Point3f> &pts2,cv::Mat &R, cv::Mat &t){typedef g2o::BlockSolverX BlockSolverType;typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType;auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));g2o::SparseOptimizer optimizer; // graph modeloptimizer.setAlgorithm(solver); // set solveroptimizer.setVerbose(true); // print infobcv::VertexPose *p = new VertexPose();p->setId(0);p->setEstimate(Sophus::SE3d());optimizer.addVertex(p);// add edgefor(size_t i = 0; i < pts1.size(); i++) {bcv::EdgeProjectXYZRGBDPoseOnly *e = new bcv::EdgeProjectXYZRGBDPoseOnly(Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z));e->setVertex(0, p);e->setMeasurement(Eigen::Vector3d(pts1[i].x, pts1[i].y, pts1[i].z));e->setInformation(Eigen::Matrix3d::Identity());optimizer.addEdge(e);}auto t1 = std::chrono::system_clock::now();optimizer.initializeOptimization();optimizer.optimize(10);auto t2 = std::chrono::system_clock::now();auto d = std::chrono::duration_cast<std::chrono::milliseconds>(t2 - t1).count();std::cout << "duration: " << d << " ms" << std::endl;std::cout << "after optim:\n";std::cout << "T=\n" << p->estimate().matrix() << std::endl;Eigen::Matrix3d R_ = p->estimate().rotationMatrix();Eigen::Vector3d t_ = p->estimate().translation();std::cout <<"det(R_)=" << R_.determinant() << std::endl;std::cout <<"R_R_^T=" << R_ * R_.transpose() << std::endl;std::cout << "R:\n" << R_ << std::endl;std::cout << "t:\n" << t_ << std::endl;R = (cv::Mat_<double>(3, 3) <<R_(0, 0), R_(0, 1), R_(0, 2),R_(1, 0), R_(1, 1), R_(1, 2),R_(2, 0), R_(2, 1), R_(2, 2));t = (cv::Mat_<double>(3, 1) << t_(0, 0), t_(1, 0), t_(2, 0));}

完整可运行代码见https://gitee.com/lx_r/basic_cplusplus_examples

• 1.视觉SLAM十四讲第二版p196-198