6.1 树概念及结构

6.1.1 树的概念

类似八股文一样的东西，需要记一下。

树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

• 有一个特殊的结点，称为根结点，根节点没有前驱结点

• 除根节点外，其余结点被分成$M(M>0)$个互不相交的集合$T_1$、$T_2$、……、$T_m$，其中每一个集合$T_i(1\le i\le m)$又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继

• 因此，树是递归定义的。树将一个整体分成若干个根和子树。

注意：树形结构中，子树之间不能有交集，否则就不是树形结构，在数据结构中这种有交集的树不再是树，而是图。

关于树，结点和节点指同一个东西。虽然节点更像是通过输入法打字造成的错词。

6.1.2 树的术语解读

关于树：树的概念参照树+人类亲缘关系描述。

现代计算机基本起源于欧美，翻译上可能存在争议和社会色彩。无论什么样的翻译，不影响学习即可。

节点的度：一个节点含有的子树的个数称为该节点的度； 如图：A的为6。

叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点。

除了叶结点都是分支结点。

非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点。

A既是分支结点，又是根结点，它可以有多重身份。

双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点。

孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点。

兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点。

除了亲兄弟，还有堂兄弟结点表示它们是同辈分但不一定是一样的父结点，比如H，I。这种说法不常用。

树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6（A，E，I，J，P，Q六个结点）。

节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；

树的高度或深度：树中节点的最大层次； 如上图：树的高度为4。

1个结点的树高（层次）为1，空树的树高为0，这是以根结点为第一层来定义的。

若按根结点为第0层算，则空树树高为-1。

一般根结点的树高为1更常用。

堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点。

节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先。

子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙。

森林：由$m(m>0)$棵互不相交的树的集合称为森林。

6.1.3 树的表示

树结构既然保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。

我们这里就简单的了解其中最常用的孩子兄弟表示法（有人也叫左孩子右兄弟表示法）。

typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};

孩子兄弟表示法可以表示任何树型数据结构。电脑中的树的应用就是文件系统。

Linux操作系统用斜杠/表示根目录。

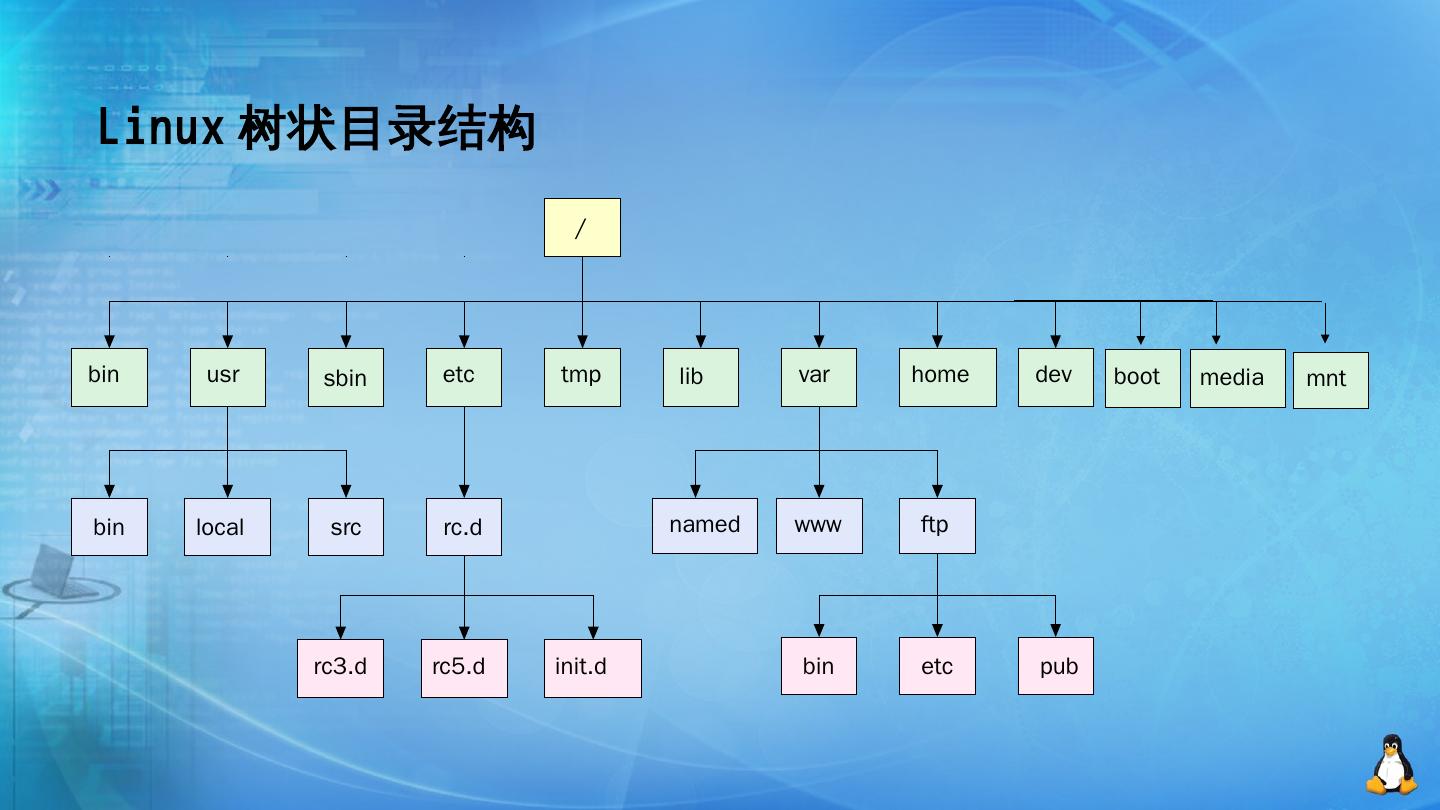
windows操作系统的目录结构是森林或一棵树。windows的树使用的孩子兄弟表示法。

点击进入某个文件夹即为链表的遍历。

添加文件夹本质是在最后一个兄弟结点后插入一个结点。